stopień trudności: średnio trudny
czas pisania: 45 minut
przeznaczenie: zestaw może być wykorzystany na sprawdzianie, do pracy na lekcji (np. w parach) lub jako zadanie domowe
ocenianie:
25 - 30 - bardzo dobry
20 - 24 - dobry
15 - 19 - dostateczny
10 - 14 - dopuszczający
0 - 9 - niedostateczny
grupa A
W zadaniach 1-4 wybierz poprawną odpowiedź.
Zad. 1. (1 pkt) W którym zestawie danych mediana jest równa 6?
I. 1, 2, 2, 6, 8, 9 12
II. 2, 3, 3, 4, 5, 7, 8, 14, 15, 15
III. 3, 4, 6, 6, 6, 7, 8, 8, 9, 12, 13
IV. 1, 1, 1, 1, 1, 7, 7, 7, 7 ,7
A) tylko w I i II B) tylko w II i IV C) tylko w III D) tylko w I, II i IV
Zad. 2. (1 pkt) Do zestawu liczb 2, 4, 5, 7, 14, 14 dopisano jeszcze jedną liczbę. Średnia powiększonego zestawu wynosi 9. Jaką liczbę dopisano?
A) 9 B) 23 C) 17 D) nie ma takiej liczby
Zad. 3. (1 pkt) W urnie znajduje się jedna kula czerwona i trzy niebieskie. Losujemy kolejno trzy kule, za każdym razem zwracając je po losowaniu do urny. Zdarzeniem niemożliwym jest:
A) wylosowanie trzech kul czerwonych
B) wylosowanie trzech kul niebieskich
C) wylosowanie trzech kul w trzech różnych kolorach
D) wylosowanie dwóch kul czerwonych i jednej niebieskiej
Zad. 4. (1 pkt) Rysunek wskazuje liczbę i kolor (biały, czarny, szary) kul znajdujących się w czterech pudełkach. Losujemy po jednej kuli z każdego pudełka.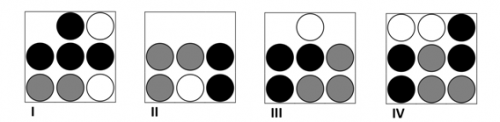
Z którego pudełka prawdopodobieństwo wylosowania kuli czarnej jest największe?
A) I B) II C) III D) IV i II
W zadaniach 5 i 6 uzupełnij luki, wybierając odpowiedzi spośród podanych.
Zad. 5. (3 pkt) Cztery przyjaciółki otrzymywały od rodziców miesięczne kieszonkowe: Ania - 90 zł, Kasia - 80 zł, Zosia - 60 zł, a Paulina - 70 zł. Od 1 stycznia roku rodzice Kasi i Pauliny podnieśli im wypłaty i teraz średnia wysokość kieszonkowego czwórki przyjaciółek wynosi 90 zł. Paulina dostała podwyżkę o 100% większą niż Kasia.
a) Średnia wysokość kieszonkowego dziewczynek przed 1 stycznia wynosiła … zł.
b) Rozstęp wysokości kieszonkowego przyjaciółek po 1 stycznia wynosi … zł.
c) Mediana wysokości kieszonkowego po podwyżce równa się … zł
A) 75 B) 100 C) 30 D) 50 E) 105 F) 90 G) 95 H) nie da się ustalić
Zad. 6. (3 pkt) W urnie jest jedna kula niebieska i jedna zielona. Losujemy jedna kulę, zwracamy ja do urny i ponownie losujemy kulę.
a) Liczebność zbioru zdarzeń elementarnych jest równa …
b) Prawdopodobieństwo, że wylosowano jedną kulę zieloną i jedną niebieską równa się …
c) Prawdopodobieństwo, że wylosowano jako pierwszą kulę zieloną a jako drugą - niebieską równa się …
A) 1/4 B) 1/2 C) 4 D) 3 E) 2 F) 1/3 G) nie da się ustalić
W zadaniach 7-9 oceń prawdziwość odpowiedzi, oznaczając przez P - zdania prawdziwe, a przez F - fałszywe.
Zad. 7. (5 pkt) W tabeli przedstawiono końcoworoczne oceny z matematyki uczniów klasy 3A.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba uczniów | 3 | 5 | 9 | 8 | 6 | 1 |
A) Średnia ocen wynosi 3.
B) Mediana ocen jest równa 3.
C) Klasa liczy 32 osoby.
D) Moda ocen wynosi 3.
E) Rozstęp ocen równy jest 2.
Zad. 8. (3 pkt). Doświadczenie losowe polega na rzucie monetą, a następnie sześcienną kostką do gry.
A) Jest 12 możliwych wyników tego doświadczenia.
B) Zdarzeniem pewnym jest wylosowanie orła lub reszki i liczby dwucyfrowej.
C) Zdarzeniem możliwym jest wylosowanie orła i liczby pierwszej.
Zad. 9. (4 pkt) Na diagramie przedstawiono dane dotyczące liczby zwierząt posiadanych przez uczniów klasy 3A.
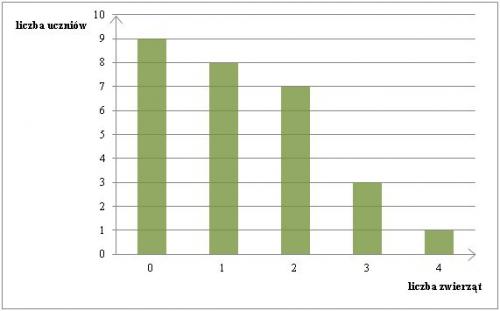
A) Klasa liczy 28 uczniów.
B) Średnia liczba posiadanych zwierząt wynosi 1.
C) Ponad połowa uczniów ma więcej zwierząt niż wynosi średnia.
D) Mediana przedstawionych danych wynosi 1.
W zadaniach 10 -12 odpowiedz na pytania i zapisz obliczenia.
Zad. 10. (2 pkt) Średni miesięczny dochód firmy pana Kowalskiego w pierwszym półroczu 2014 roku wyniósł 2 tys. zł. Podaj modę miesięcznego dochodu tej firmy, wiedząc, że przez pięć miesięcy przynosiła ona zyski, a w szóstym miesiącu zanotowano 0,5 tys. zł straty. Przez pierwsze cztery miesiące dochód był stały. Rozstęp miesięcznych dochodów wynosił 5 tys. zł.
Zad. 11. (3 pkt) W urnie znajdują się cztery kule zielone i sześć czarnych. Losujemy kolejno dwie kule bez zwracania do pojemnika. Narysuj drzewko probabilistyczne dla tego doświadczenia oraz oblicz prawdopodobieństwo zdarzenia Z, polegającego na wylosowaniu dwóch kul zielonych.
Zad. 12. (3 pkt) Z pojemnika, w którym jest 8 losów wygrywających i 5 pustych, losujemy dwa razy po jednym losie bez zwracania. Narysuj drzewko probabilistyczne dla tego doświadczenia i oblicz prawdopodobieństwo, że wyciągniemy co najmniej jeden los wygrywający.
grupa B
W zadaniach 1-4 wybierz poprawną odpowiedź.
Zad. 1. (1 pkt) W których zestawach danych mediana jest równa 8?
I. 1, 1, 2, 6, 8, 9 12, 13 nie
II. 2, 3, 3, 4, 5, 7, 9, 9,14, 14, 15, 15 tak
III. 3, 4, 6, 6, 6, 7, 8, 8, 9, 12, 13 nie
IV. 1, 1, 1, 1, 1, 15, 16, 17, 17 ,17
A) tylko w I B) tylko w II i IV C) tylko w II D) tylko w II, III i IV
Zad. 2. (1 pkt) Do zestawu liczb 1, 6, 8, 13, 13 dopisano jeszcze jedną. Średnia powiększonego zestawu wynosi 7. Jaką liczbę dopisano?
A) 2 B) 7 C) 1 D) nie ma takiej liczby
Zad. 3. (1 pkt) W urnie znajdują się trzy kule białe i jedna czarna. Losujemy kolejno trzy kule, zwracając je do urny po każdym losowaniu. Zdarzeniem niemożliwym jest:
A) wylosowanie trzech kul białych
B) wylosowanie trzech kul czarnych
C) wylosowanie dwóch kul białych i jednej czarnej
D) wylosowanie trzech kul w trzech różnych kolorach
Zad. 4. (1 pkt) Rysunek wskazuje liczbę i kolor (biały, czarny, szary) kul znajdujących się w czterech pudełkach. Losujemy po jednej kuli z każdego pudełka. 
Z którego pudełka prawdopodobieństwo wylosowania kuli szarej kuli jest największe?
A) I B) II C) III D) IV i III
W zadaniach 5 i 6 uzupełnij luki, wybierając odpowiedzi spośród podanych.
Zad. 5. (3 pkt) Czterech kolegów otrzymywało od rodziców miesięczne kieszonkowe: Adam - 100 zł, Jakub - 80 zł, Piotrek - 90 zł i Filip - 70 zł. Od 1 stycznia rodzice Filipa i Piotrka podnieśli im wypłaty. Teraz średnia wysokość kieszonkowego czwórki chłopców wynosi 100 zł. Filip dostał podwyżkę o 100% większą niż Piotrek.
a) Średnia wysokość kieszonkowego chłopców przed 1 styczniem wynosiła … zł.
b) Rozstęp wysokości kieszonkowego chłopców po 1 stycznia wynosi … zł.
c) Mediana wysokości kieszonkowego po podwyżce równa się … zł.
A) 75 B) 105 C) 30 D) 50 E) 100 F) 85 G) 110 H) nie da się ustalić
Zad. 6. (3 pkt) W urnie jest jedna kula biała i jedna czarna. Losujemy jedna kulę, zwracamy ją do urny i ponownie losujemy.
a) Liczebność zbioru zdarzeń elementarnych jest równa …
b) Prawdopodobieństwo, że wylosowano jedną kulę czarną i jedną białą równa się…
c) Prawdopodobieństwo, że wylosowano jako pierwszą kulę czarną, a jako drugą białą równa się …
A) 1/4 B) 2 C) 3 D) 4 E) 1/2 F) 1/3 G) nie da się ustalić
W zadaniach 7-9 oceń prawdziwość odpowiedzi, oznaczając przez P - zdania prawdziwe, a przez F - fałszywe.
Zad. 7. (5 pkt) W tabeli przedstawiono oceny końcoworoczne z matematyki uczniów klasy 3B.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba uczniów | 2 | 4 | 7 | 8 | 6 | 2 |
A) Średnia ocen wynosi 4.
B) Mediana ocen jest równa 3.
C) Klasa liczy 29 osób.
D) Moda ocen wynosi 4.
E) Rozstęp ocen jest równy 0.
Zad. 8. (3 pkt) Doświadczenie losowe polega na dwukrotnym rzucie monetą, a następnie sześcienną kostką do gry.
A) Są 24 możliwe wyniki tego doświadczenia.
B) Zdarzeniem pewnym jest wylosowanie dwa razy orła i liczby dodatniej mniejszej od 7.
C) Zdarzeniem możliwym jest wylosowanie dwa razy reszki i liczby złożonej.
Zad. 9. (4 pkt) Na diagramie przedstawiono dane dotyczące liczby zwierząt posiadanych przez uczniów klasy 3B.
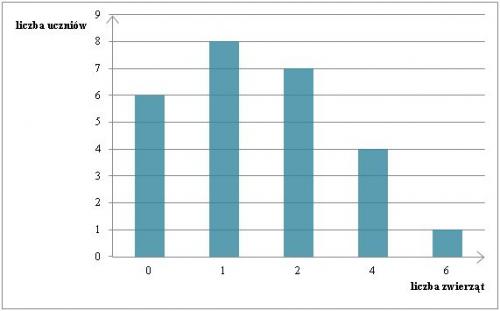
A) Klasa liczy 26 osób.
B) Średnia liczba posiadanych zwierząt wynosi 2.
C) Ponad połowa uczniów ma więcej zwierząt niż wnosi średnia.
D) Mediana przedstawionych danych wynosi 1.
W zadaniach 10-12 odpowiedz na pytania i zapisz obliczenia.
Zad. 10. (2 pkt) Średni miesięczny dochód firmy pana Nowaka w drugim półroczu 2014 roku wyniósł 3 tys. zł. Podaj modę miesięcznego dochodu tej firmy, wiedząc, że przez pięć miesięcy firma przynosiła zyski, a w szóstym zanotowano 1 tys. zł straty. Przez 4 pierwsze miesiące dochód był stały. Rozstęp miesięcznych dochodów wynosił 5 tys. zł.
Zad. 11. (3 pkt) W pojemniku znajduje się sześć bil czerwonych i cztery niebieskie. Losujemy kolejno dwie bile bez zwracania ich do pojemnika. Narysuj drzewko probabilistyczne tego doświadczenia oraz oblicz prawdopodobieństwo zdarzenia C, polegającego na wylosowaniu dwóch bil czerwonych.
Zad. 12. (3 pkt) Z pojemnika, w którym są cztery losy wygrywające i osiem pustych, losujemy dwa razy po jednym losie bez zwracania. Narysuj drzewko probabilistyczne tego doświadczenia i oblicz prawdopodobieństwo, że wyciągniemy co najmniej jeden los wygrywający.
odpowiedzi
Grupa A
1. A, 2. C, 3. C, 4. A, 5. a) A, b) D, c) G, 6. a) C, b) B, c) A, 7. F, P, P, P, F, 8. P, F, P, 9. P, F, F, P, 10. 1,75 tys. zł, 11. P(Z) = 2/15, 12. p= 34/39
Grupa B
1. B, 2. C, 3. D, 4. B, 5. a) F, b) C, c) B, 6. a) D, b) E, c) A, 7. F, F, P, P, F, 8. P, F, P, 9. P, F, F, P, 10. 3,25 tys. zł, 11. P(C) = 1/3, 12. p= 19/33
kryteria oceniania
1. - 4. 1 pkt za odpowiedź
5. - 6. 1 pkt za każdą odpowiedź
7. - 9. 1 pkt za każdą odpowiedź
10. 1 pkt za ustalenie wysokości dochodów w każdym miesiącu, 1 pkt za odpowiedź
11. 1 pkt za rysunek drzewka z podanymi prawdopodobieństwami, 1 pkt za sposób obliczania, 1 pkt za odpowiedź
12. 1 pkt za rysunek drzewka z podanymi prawdopodobieństwami,1 pkt za sposób obliczania, 1 pkt za odpowiedź






 Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było?
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 


błedne odpowiedzi
WITAM SERDECZNIE. w wyżej zadaniach zauważyłam w rozwiązaniach błędy.A mianowicie w teście B. ZAD 9 w podpunkcie A) klasa liczy 25 uczniów I TO JEST WEDŁUG WAS prawda , podana odpowiedz jest 25 a mnie wychodzi 26 według diagramu bo 6+8+7+4+1=26 i to samo w zadaniu 7 liczba uczniów =29 a nie 30.Natomiast w zadaniu z grupy A ZAD 1 poprawna odpowiedz jest A a zaznaczona D.Mam ogromna prośbę o sprawdzenie tych odpowiedzi
Dziękuję, poprawiłam.
Dziękuję, poprawiłam.