stopień trudności: średnio trudny
czas pisania: 45 minut
przeznaczenie: zestaw może być wykorzystany na sprawdzianie, do pracy na lekcji (np. w parach) lub jako zadanie domowe
ocenianie:
25 - 30 - bardzo dobry
20 - 24 - dobry
15 - 19 - dostateczny
10 - 14 - dopuszczający
0 - 9 - niedostateczny
grupa A
W zadaniach 1-4 wybierz jedną poprawną odpowiedź.
Zad. 1. (1 pkt) Na okręgu o środku w punkcie (0,0) i promieniu 5 leży punkt:
A) (1,4) B) (-5,1) C) (-1, 2√3) D) (-2√6,1)
Zad. 2. (1 pkt) ) Jeden z boków kwadratu wydłużono o 20%, a drugi – równoległy do niego - skrócono o 20% w taki sposób, że otrzymano trapez prostokątny. Pole trapezu jest:
A) większe od pola kwadratu o 20%.
B) równe polu kwadratu.
C) równe 64% pola kwadratu.
D) równe 96% pola kwadratu.
Zad. 3. (1 pkt) W trójkącie prostokątnym jeden z kątów ma rozwartość 30°, a krótsza przyprostokątna ma długość 8. Wysokość opuszczona na przeciwprostokątną ma długość:
A) 8√3 B) 4√3 C) 8 D) niemożliwą do obliczenia.
Zad. 4. (1 pkt) W trójkącie prostokątnym o bokach długości 6 cm, 8 cm i 10 cm zwiększono przyprostokątne o 1 cm. Długość przeciwprostokątnej wzrosła się o:
A) 1 cm B) √130 cm C) (√130 -10) cm D) 2 cm.
W zadaniach 5-6 uzupełnij luki, wybierając odpowiedzi spośród podanych.
Zad. 5. (3 pkt.) Jeden z kątów rombu ma miarę 120°, a długość jego boku równa się 6.
a) Krótsza przekątna rombu ma długość … .
b) Pole rombu równa się… .
c) Wysokość rombu równa się … .
A) 12√3 B) 6√3 C) 3 D) 3√3 E) 40,5√3 F) 18√3 G) 6
Zad. 6. (4 pkt.) Na rysunkach przedstawiono trapez ABCD, trójkąt EFG i dwie proste równoległe a i b. Miary kątów wynoszą: a) α=… b) β=… c) γ=… d) δ=….
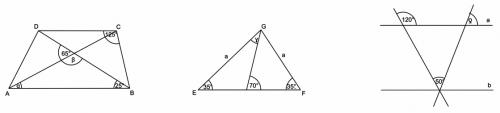
A) 25° B) 70° C) 60° D) 115° E) 40° F) 35° G) 50° H) 125° I) 135°
W zad. 7. wybierz jedną poprawną odpowiedź oraz jej uzasadnienie.
Zad. 7. (2 pkt.) Dwa okręgi o promieniu 2 i środkach C, D przecinają się w różnych punktach E i F. Czy prosta EF jest symetralną odcinka CD?
a) Tak, b) Nie,
ponieważ
A) Prosta EF dzieli odcinek CD na dwie równe części.
B) Prosta EF jest prostopadła do odcinka CD.
C) Trójkąty CFD i CED są przystające i równoboczne.
D) Trójkąty CFD i CED są przystające i równoramienne.
W zadaniach 8-9 oceń prawdziwość odpowiedzi, oznaczając przez P - zdania prawdziwe, a przez F - fałszywe.
Zad. 8. (4 pkt.)
A) Środek okręgu opisanego na trójkącie ostrokątnym leży w przecięciu dwusiecznych jego kątów.
B) Promień okręgu opisanego na trójkącie równobocznym o boku równym 12 cm ma 4√3 cm.
C) Pole koła opisanego na sześciokącie foremnym o boku długości a równa się πa2.
D) Suma długości promieni okręgu opisanego i wpisanego w kwadrat o boku długości 2 cm równa się (√2 +1) cm.
Zad. 9. (4 pkt.)
A) Prosta ma nieskończenie wiele środków symetrii.
B) Trójkąt równoboczny ma jeden środek symetrii.
C) Prostokąt ma 4 osie symetrii.
D) Romb ma 2 osie symetrii i 1 środek symetrii.
W zadaniach 10 -12 odpowiedz na pytania i zapisz rozumowanie oraz obliczenia.
Zad. 10. (2 pkt.) Uzasadnij, że środki boków dowolnego trójkąta równobocznego są wierzchołkami innego trójkąta równobocznego.
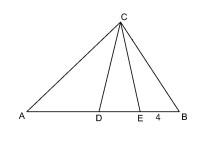
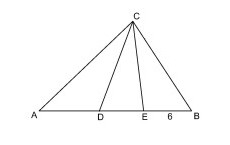
Zad. 11. (3 pkt.) Pole trójkąta ADC jest trzy razy większe od pola trójkąta EBC i sześć razy większe od pola trójkąta DEC. Oblicz długości odcinków AD i DE.
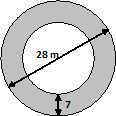
Zad. 12. (4 pkt.) Zamalowaną na planie część działki pani Ewa przeznaczyła na trawnik. Ile opakowań trawy uniwersalnej Cambridge powinna kupić, jeśli 1 kg nasion wystarcza na obsianie 42 m2 powierzchni, a opakowania nasion waży 3 kg? W obliczeniach przyjmij π=3.
grupa B
W zadaniach 1-4 wybierz jedną poprawną odpowiedź.
Zad. 1. (1 pkt) Na okręgu o środku w punkcie (0,0) i promieniu 7 leży punkt:
A) (1,6) B) (-7,1) C) (16, 2√3) D) (-4√3,1)
Zad. 2. (1 pkt) Jeden z boków kwadratu wydłużono o 10%, a drugi - równoległy do niego - skrócono o 10% w taki sposób, że otrzymano trapez prostokątny. Pole trapezu jest:
A) większe od pola kwadratu o 10%.
B) równe polu kwadratu.
C) równe 81% pola kwadratu.
D) równe 99% pola kwadratu.
Zad. 3. (1 pkt) W trójkącie prostokątnym jeden z kątów ma rozwartość 60°, a krótsza przyprostokątna ma długość 4. Wysokość opuszczona na przeciwprostokątną ma długość:
A) 4√3 B) 2√3 C) 2 D) niemożliwa do obliczenia.
Zad. 4. (1 pkt) W trójkącie prostokątnym o bokach długości 5 cm, 12 cm i 13 cm zwiększono przyprostokątne o 1 cm. Długość przeciwprostokątnej wzrosła o:
A) 1 cm B) √205 cm C) (√205 -13) cm D) 2 cm
W zadaniach 5-6 uzupełnij luki, wybierając odpowiedzi spośród podanych.
Zad. 5. (3 pkt.) Jeden z kątów rombu ma miarę 120°, a długość jego boku równa się 8.
a) Krótsza przekątna rombu ma długość … .
b) Pole rombu równa się… .
c) Wysokość rombu równa się … .
A) 16√3 B) 8√3 C) 4 D) 4√3 E) 64√3 F) 32√3 G) 8
Zad. 6. (4 pkt.) Na rysunkach mamy trapez ABCD, trójkąt EFG i dwie proste równoległe a i b. Miary kątów wynoszą: a) α=… b) β=… c) γ=… d) δ=….
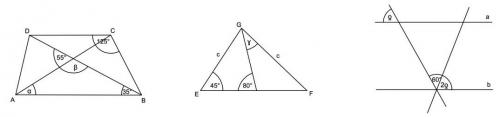
A) 25° B) 40° C) 60° D) 20° E) 125° F) 35° G) 45° H) 115° I) 135°
W zad. 7. wybierz jedną poprawną odpowiedź i jej uzasadnienie.
Zad. 7. (2 pkt.) Dwa okręgi o promieniu 1 i środkach R, S przecinają się w różnych punktach A i B. Czy prosta AB jest symetralną odcinka RS?
a) Tak, b) Nie,
ponieważ
A) Prosta AB jest prostopadła do odcinka RS.
B) Trójkąty RSA i RSB są przystające i równoramienne.
C)Trójkąty RAS i RBS są przystające i równoboczne.
D) Prosta AB dzieli odcinek RS na dwie równe części.
W zadaniach 8-9 oceń prawdziwość odpowiedzi, oznaczając przez P - zdania prawdziwe, a przez F - fałszywe.
Zad. 8. (4 pkt.)
A) Środek okręgu opisanego na trójkącie rozwartokątnym leży na jego najdłuższym boku.
B) Promień okręgu wpisanego w trójkąt równoboczny o boku równym 6 cm ma √3 cm.
C) W kwadrat o przekątnej 6√2 cm wpisano koło. Pole tego koła równa się 9π cm2.
D) Promień okręgu wpisanego w sześciokąt foremny równa się długości jego boku.
Zad. 9. (4 pkt.)
A) Okrąg ma nieskończenie wiele osi symetrii.
B) Półprosta ma 2 osie symetrii.
C) Równoległobok ma co najmniej jedną oś symetrii.
D) Figura złożona z dwóch prostych równoległych ma nieskończenie wiele środków symetrii.
W zadaniach 10-12 odpowiedz na pytania i zapisz rozumowanie oraz obliczenia.
Zad. 10. (2 pkt.) Uzasadnij, że środki boków dowolnego prostokąta są wierzchołkami rombu.
Zad. 11. (3 pkt.) Pole trójkąta ADC jest dwa razy większe od pola trójkąta EBC i cztery razy większe od pola trójkąta DEC. Oblicz długości odcinków AD i DE.
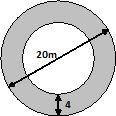
Zad. 12. (4 pkt.) Zamalowaną na planie część działki pani Ania przeznaczyła na trawnik. Ile opakowań trawy uniwersalnej Oxford powinna kupić, jeśli 1 kg nasion wystarcza na obsianie 40 m2 powierzchni, a opakowanie nasion waży 1,5 kg? W obliczeniach przyjmij π=3.
odpowiedzi:
grupa A
1. D 2. B 3. B 4. C 5. G, F, D 6. E, D, F, B 7. a, D 8. FPPP 9. PFFP
10. Boki utworzonego trójkąta są jednocześnie bokami trzech trójkątów równobocznych przystających na podstawie cechy b,k,b.
11. AD=12, DE=2
12. R=14 m, r=7 m, pole pierścienia ≈ 441, waga nasion = 10,5 kg, 4 opakowania.
grupa B
1. D 2. B 3. B 4. C 5. G, F, D 6. E, D, F, B 7. a, B 8. FPPF 9. PFFP
10. Boki utworzonego czworokąta są jednocześnie bokami czterech trójkątów przystających na podstawie cechy b,k,b.
11. AD=12, DE=3
12. R=10 m, r=6 m, pole pierścienia ≈ 192, waga nasion = 4,8 kg, 4 opakowania.
Kryteria oceniania:
1-9. 1 pkt za odpowiedź
5-9. 1 pkt za każdą odpowiedź
10. 1 pkt za znalezienie trójkątów przystających i uzasadnienie przystawania, 1 pkt za sformułowanie wniosku.
11. 1 pkt za zauważenie, że wszystkie trójkąty mają wspólna wysokość, 1 pkt za równanie, 1 pkt za odpowiedź.
12. 1 pkt za ustalenie długości promieni ,1 pkt za obliczenie pola pierścienia, 1 pkt za metodę obliczania liczby opakowań nasion, 1 pkt za wynik.
