Funkcje* (kl. 3)

stopień trudności:

• podwyższony, sprawdzian przeznaczony dla klas z rozszerzonymi treściami nauczania
• zadanie z (*) obowiązkowe na ocenę celującą
• grupy A i B mają ten sam stopień trudności

ocenianie:
21-22 - celujący
18-20 - bardzo dobry
15-17 - dobry
11-14 - dostateczny
8-10 - dopuszczający
0-7 - niedostateczny

czas pisania: 45 minut

typ sprawdzianu: sprawdza wiadomości po zakończeniu działu tematycznego, zadania traktujemy jako otwarte, uczeń powinien przedstawić pełny tok rozumowania i rachunki

grupa A (22 pkt)

Zad. 1. (4 pkt) Dane są funkcje liniowe f: y=0,5x–4 i g: y=–x+2.
a) Sporządź wykresy funkcji f i g.
b) Oblicz pole figury ograniczonej wykresami tych funkcji oraz osią x.
c) Podaj, dla jakich argumentów funkcja f przyjmuje wartości większe niż funkcja g.

Zad. 2. (4 pkt) Reklama świetlna składa się z pięciu części różnych kolorów. Każdy stan reklamy trwa 3 sekundy. Najpierw jest ciemno, potem świeci jeden kolor, potem dwa, potem trzy, potem cztery, potem pięć, a następnie gasną w odwrotnej kolejności niż się zapalały i cały proces zaczyna się od początku. Niech t oznacza czas w sekundach, a n – liczbę barw świecących się w reklamie. Funkcja f określa n w zależności od t.
a) Narysuj wykres funkcji f.
b) Podaj zbiór wartości tej funkcji.
c) Jaki jest stan reklamy po upływie 44 sekund?
d) Reklama jest włączona już 1 minutę. Po ilu najwcześniej sekundach od tego momentu reklama będzie ciemna?

Zad. 3. (3 pkt) Określ dziedzinę i narysuj wykres funkcji [tex]\small \frac{\sqrt{x^2-4x+4}}{x-2}[/tex].

Zad. 4. (3 pkt) Dla jakich wartości k punkt przecięcia wykresów funkcji liniowych y=3x–k i y=-0,5x+4 leży w I ćwiartce prostokątnego układu współrzędnych?

Zad. 5. (3 pkt) Oblicz odległość prostych y=3x i y=3x+6.

Zad. 6. (3 pkt) Określamy funkcję [tex]\small\min\{a, b\}=\left\{\begin{array}{lcl}a& dla& a\leq b\\b& dla &a>b\end{array}\right.[/tex].
a) Naszkicuj wykres funkcji [tex]\small f(x)=\min\{-3,\frac{1}{x}\}[/tex], gdzie [tex]\small x\in R\setminus\{0\}[/tex].
b) Zbadaj monotoniczność funkcji f.

Zad. 7*. (2 pkt) Wyznacz wartość parametru a tak, aby funkcja y = ||x–1|–2|–a miała trzy miejsca zerowe.

grupa B (22 pkt)

Zad. 1. (4 pkt) Dane są funkcje liniowe f: y=–x+1 i g: y=0,5x–2.
a) Sporządź wykresy funkcji f i g.
b) Oblicz pole figury ograniczonej tymi wykresami oraz osią y.
c) Dla jakich argumentów funkcja f przyjmuje wartości mniejsze niż funkcja g?

Zad. 2. (4 pkt) Reklama świetlna składa się z czterech części różnych kolorów. Każdy stan reklamy trwa 2 sekundy. Najpierw jest ciemno, potem świeci jeden kolor, potem dwa, potem trzy, potem cztery, a następnie gasną w odwrotnej kolejności niż się zapalały i cały proces zaczyna się od początku. Niech t oznacza czas w sekundach, a n – liczbę barw świecących się w reklamie. Funkcja f określa n w zależności od t.
a) Narysuj wykres funkcji f.
b) Podaj zbiór wartości tej funkcji.
c) Jaki jest stan reklamy po upływie 39 sekund?
d) Reklama jest włączona już 1 minutę. Po ilu sekundach najwcześniej sekundach od tego momentu reklama będzie ciemna?

Zad. 3. (3 pkt) Określ dziedzinę i narysuj wykres funkcji [tex]\small \frac{\sqrt{x^2-6x+9}}{x-3}[/tex].

Zad. 4. (3 pkt) Dla jakich wartości k punkt przecięcia wykresów funkcji liniowych y=2x+k i y=0,5x+2 leży w III ćwiartce prostokątnego układu współrzędnych?

Zad. 5. (3 pkt) Oblicz odległość prostych y=2x i y=2x+2.

Zad. 6. (3 pkt) Określamy funkcję [tex]\small\max\{a,b\}=\left\{\begin{array}{rcl}a& dla& a\geq b\\b & dla & a<b\end{array}\right.[/tex].
a) Naszkicuj wykres funkcji [tex]\small f(x)=\max\{2,\frac{-1}{x}\}[/tex], gdzie [tex]\small x\in R\setminus\{0\}[/tex].
b) Zbadaj monotoniczność funkcji f.

Zad. 7*. (2 pkt) Wyznacz wartość parametru a tak, aby funkcja y = ||x–2|–3|–a miała cztery miejsca zerowe.

odpowiedzi

grupa A
1. b) pole=6 j², c) f(x)>g(x) dla x>4
2. a)

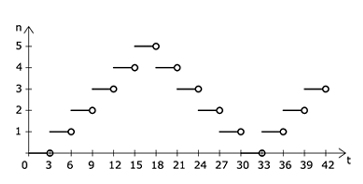
b) {0, 1, 2, 3, 4, 5}, c) 4 kolory, d) po zeru sekundach
3. dziedzina = R\{2}, [tex]\small y=\left\{\begin{array}{rcl}1& dla & x>2\\-1& dla &x<2\end{array}\right.[/tex]
4. -4 < k< 24
5. [tex]\small 0,6\sqrt{10}[/tex]
6. a)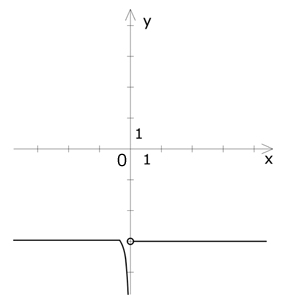
[tex]\small y= \left\{\begin{array}{rcl}-3& dla & x \geq\frac{-1}{3}\\ \frac{1}{x}& dla & \frac{-1}{3}<x<0 \\ -3 & dla & x>0\end{array}\right.[/tex]
b) funkcja malejąca dla [tex]\small \frac{-1}{3}<x<0[/tex], funkcja stała dla [tex]\small x<\frac{-1}{3}[/tex] lub x >0
7. a = 2

grupa B
1. b) pole=3 j², c) f(x)>g(x) dla x>2
2. a)

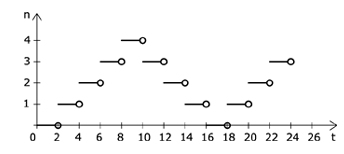
b) {0, 1, 2, 3}, c) 4 kolory, d) po czterech sekundach
3. dziedzina = R\{3}, [tex]\small y =\left\{\begin{array}{rcl}1 & dla & x>3\\-1 & dla & x<3\end{array}\right.[/tex]
4. k>8
5. 0,4√5
6. a)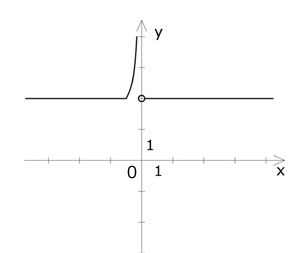

[tex]\small y= \left\{\begin{array}{rcl}2 & dla & x \geq\frac{-1}{2}\\
\frac{-1}{x}& dla & \frac{-1}{2}<x<0 \\ 2 & dla &
x>0\end{array}\right.[/tex]
b) funkcja rosnąca dla [tex]\small \frac{-1}{2}<x<0[/tex], stała dla [tex]\small x<\frac{-1}{2}[/tex] lub x > 0
7. 0< a < 3

kryteria oceniania
1. a) 1 pkt za wykresy funkcji, 1 pkt za obliczenie punktu ich przecięcia, b) 1 pkt za pole, c) 1 pkt za odpowiedź
2. a) – d) po 1 punkcie
3. 1 pkt za dziedzinę, 1 pkt za wzór funkcji bez znaku pierwiastka, 1 pkt za wykres
4. 1 pkt za wyznaczenie k w zależności od x, 1 pkt za wyznaczenie k w zależności od y, 1 pkt za odpowiedź
5. 1 pkt za rysunek z zaznaczoną odległością drugiej prostej od początku układu współrzędnych, 1 pkt za wyznaczenie długości boków trójkąta utworzonego przez tą prostą i osie układu współrzędnych, 1 pkt za obliczenie wysokości, licząc na dwa sposoby pole trójkąta
6. 1 pkt za wykresy obu funkcji w układzie współrzędnych, 1 pkt za szkic wykresu funkcji minimum/maksimum, 1 pkt za podanie przedziałów monotoniczności
7. 1 pkt za rysunek lub wzór funkcji bez wartości bezwzględnej, 1 pkt za odpowiedź