Funkcje (kl. 3)

stopień trudności:

• średnio trudny
• zadanie z (*) obowiązkowe na ocenę celującą
• grupy A i B mają ten sam stopień trudności

ocenianie:
21 - celujący
18-20- bardzo dobry
14-17 - dobry
10-13 - dostateczny
7-9 - dopuszczający
0-6 - niedostateczny

czas pisania: 45 minut

typ sprawdzianu:

• sprawdzający wiadomości po zakończeniu działu tematycznego, uczeń powinien przedstawić pełny tok rozumowania i obliczenia
• może być wykorzystany jako powtórzenie wiadomości z danego działu przed testem kompetencji
   

grupa A (21 pkt)

Zad. 1. (3 pkt) Narysuj wykres funkcji y = 4–x, której dziedziną jest zbiór X = {-1, 0, 2}.

Zad. 2. (6 pkt) Rysunek przedstawia wykres funkcji f(x).

Korzystając z niego, podaj:
a) dziedzinę funkcji,
b) zbiór wartości funkcji,
c) miejsca zerowe funkcji,
d) zbiór argumentów, dla których funkcja przyjmuje wartości dodatnie,
e) przedziały argumentów, w których funkcja jest rosnąca, malejąca oraz stała,
f) argumenty, dla których wartość funkcji jest największa oraz najmniejsza.

Zad. 3. (6 pkt) Narysuj wykres funkcji podanej wzorem y = –2x+4, gdy dziedziną jest zbiór liczb rzeczywistych, a następnie podaj:
a) miejsce zerowe tej funkcji,
b) argumenty, dla których funkcja przyjmuje wartości dodatnie,
c) argument, dla którego wartość funkcji wynosi 6,
d) miejsce przecięcia z osią y,
e) czy funkcja jest rosnąca czy malejąca.

Zad.4. (2 pkt) Z kranu wyciekają 4 ml wody w ciągu sekundy. Zapisz wzór wyrażający zależność objętości wody, która wyciekła z kranu (y) od czasu (x).

Zad. 5. (3 pkt) Pole rombu równa się 18 cm². Zapisz zależność między jego przekątnymi w postaci funkcji. Narysuj jej wykres, przyjmując, że długości przekątnych są liczbami naturalnymi.

Zad.6 .* (1 pkt) Podaj miejsca zerowe funkcji y = 2x³ + x²–2x–1.

grupa B (21 pkt)

Zad.1. (3 pkt) Narysuj wykres funkcji y = 3–x, której dziedziną jest zbiór X = {–2, 0, 3, 4}.

Zad. 2. (6 pkt) Rysunek przedstawia wykres funkcji f(x).

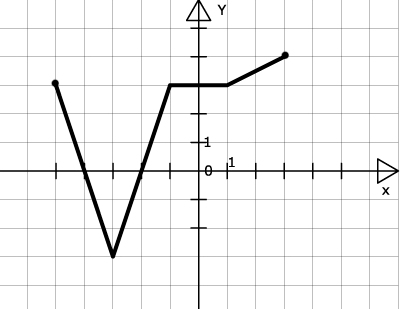
Korzystając z niego, podaj:
a) dziedzinę funkcji,
b) zbiór wartości funkcji,
c) miejsca zerowe funkcji,
d) zbiór argumenty, dla których funkcja przyjmuje wartości dodatnie,
e) przedziały argumentów, w których funkcja jest rosnąca, malejąca oraz stała,
f) argumenty, dla których wartość funkcji jest największa oraz najmniejsza.

Zad. 3. (6 pkt) Narysuj wykres funkcji podanej wzorem y = 2x–2, gdy dziedziną jest zbiór liczb rzeczywistych, a następnie podaj:
a) miejsce zerowe tej funkcji,
b) argumenty, dla których funkcja przyjmuje wartości dodatnie,
c) argument, dla którego wartość funkcji wynosi 4,
d) miejsce przecięcia z osia y,
e) czy funkcja jest rosnąca czy malejąca.

Zad.4. (2 pkt) Po odkręceniu kranu poziom wody w zbiorniku podnosi się o 6 cm co godzinę. Zapisz wzór wyrażający zależność poziomu wody (y) od czasu (x).

Zad.5. (3 pkt) Pole prostokąta równa się 24 cm². Zapisz zależność między jego bokami w postaci funkcji. Narysuj jej wykres, przyjmując, że długości boków są liczbami naturalnymi.

Zad.6.* (1 pkt) Podaj miejsca zerowe funkcji y = 4x³+x²–4x–1.

odpowiedzi:

grupa A
1. (-1;5); (0;4); (2;2)  2. a) [-6 ;4], b) [-1;3], c) -4; -2, d) x<-4; x>-2, e) rosnąca: -3<x<-1; malejąca: x<-3; stała: -1<x<1, f) największa dla x=-3, najmniejsza dla x=4  3. a)  x=2, b) x<2, c) x=-1, d) (0;4), e) malejąca 4. y= 4x 5. y=[tex]\frac{36}{x}[/tex], wykres w I ćwiartce; punkty: (1;36), (2;18), (3;12), (4;9), (6;6), (9;4), (12;3), (18;2), (36;1) 6. po rozłożeniu na czynniki: (2x+1)(x+1)(x-1) otrzymujemy:-1; -0,5; 1

grupa B
1. (-2;5); (0;3); (3;0); (4;-1) 2. a) [-5 ;3], b) [-3;4], c) -4; -2, d) x<-4; x>-2, e) rosnąca: 3<x<-1; malejąca: x<-3; stała: -1<x<1, f) największa dla x=-3, najmniejsza dla x=3  3. a) x=1, b) x>1, c) x=3, d) (0;-2), e) rosnąca 4. y= 6x  5. y=[tex]\frac{24}{x}[/tex],  wykres w I ćwiartce; punkty: (1;24), (2;12), (3;8), 4;6), (6;4), (8;3), (12;2), (24;1) 6. po rozłożeniu na czynniki: (4x+1)(x+1)(x-1) otrzymujemy: -1; -0,25; 1

kryteria oceniania:
1. 1 pkt za wypisanie współrzędnych punktów, 2 pkt. za wykres
2. a)-f) po 1 punkcie za odpowiedź
3. 1 pkt za wykres, a)-e) po 1 punkcie za odpowiedź
4. 2 pkt za wzór
5. 1 pkt za wypisanie możliwych długości przekątnych, 1 pkt za wzór, 1 pkt za wykres
6. 1 pkt za 3 miejsca zerowe wyliczone po rozłożeniu na czynniki