stopień trudności:
- podwyższony, sprawdzian przeznaczony dla klas matematycznych
- zadanie z (*) jest obowiązkowe na ocenę celującą
- grupy A i B mają ten sam poziom
ocenianie:
21-22 - celujący
18-20 - bardzo dobry
15-17 - dobry
11-14 - dostateczny
8-10 - dopuszczający
0-7 - niedostateczny
czas pisania: 45 minut
typ sprawdzianu:
- sprawdzający wiadomości po zakończeniu działu tematycznego, wtedy zadania traktujemy jako otwarte, a uczeń powinien przedstawić pełny tok rozumowania i rachunki
- może być wykorzystany jako powtórzenie wiadomości z danego działu przed testem kompetencji.
grupa A (22 pkt)
Zad. 1. (3 pkt) W trójkącie równoramiennym ramię ma 1,3 dm długości, a podstawa jest o 3 cm krótsza. Oblicz pole tego trójkąta.
Zad. 2. (4 pkt) Oblicz długości pozostałych boków trójkątów prostokątnych z rysunku.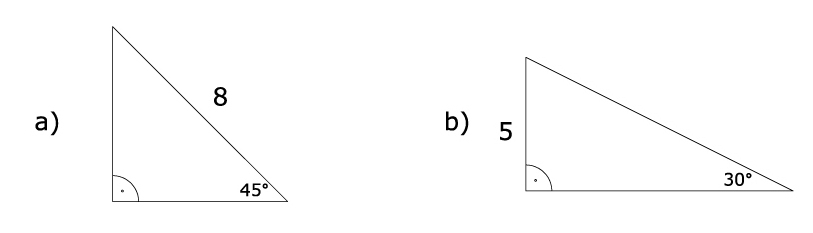
Zad. 3. (3 pkt) Dane są odcinki o długościach 3 i 4. Jaką długość z musi mieć trzeci odcinek, aby można było zbudować z nich trójkąt a) prostokątny, b) ostrokątny, c) rozwartokątny?
Zad.4. (4 pkt) W trapezie równoramiennym wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na odcinki o długościach 15 cm i 3 cm. Obwód trapezu wynosi 40 cm. Oblicz pole tego trapezu i długość jego przekątnej.
Zad. 5. (3 pkt) Oblicz obwód rombu o polu równym 24 cm2, wiedząc że stosunek długości przekątnych wynosi 3.
Zad. 6. (3 pkt) Punkt A’ jest obrazem punktu A = (1,3) w obrocie dookoła początku układu współrzędnych o kąt prosty, zgodnie z ruchem wskazówek zegara. Oblicz długość odcinka AA’.
Zad. 7*. (2 pkt) Przeciwprostokątna trójkąta prostokątnego ma długość 12 cm, a jeden z jego kątów ostrych ma miarę 60°. Oblicz długość środkowej poprowadzonej z wierzchołka tego kąta. Środkowa to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku.
grupa B (22 pkt)
Zad. 1. (3 pkt) W trójkącie równoramiennym ramię ma 1 dm długości, a podstawa jest o 2 cm dłuższa. Oblicz pole tego trójkąta.
Zad. 2. (4 pkt) Oblicz długości pozostałych boków trójkątów prostokątnych z rysunku.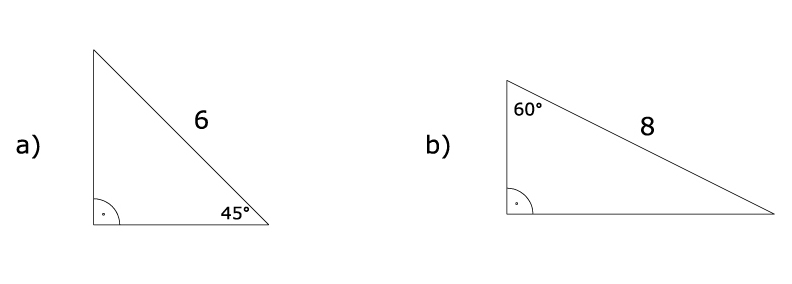
Zad. 3. (3 pkt) Dane są odcinki o długościach 6 i 8. Jaką długość z musi mieć trzeci odcinek, aby można było zbudować z nich trójkąt: a) prostokątny, b) ostrokątny, c) rozwartokątny?
Zad. 4. (4 pkt) W trapezie prostokątnym o podstawach długości 12 cm i 20 cm dłuższa przekątna ma długość 25 cm. Oblicz pole i obwód tego trapezu.
Zad. 5. (3 pkt) Oblicz obwód rombu o polu równym 16 cm2, wiedząc że stosunek długości przekątnych wynosi 2.
Zad. 6. (3 pkt) Punkt B’ jest obrazem punktu B = (3,1) w obrocie dookoła początku układu współrzędnych o kąt prosty, przeciwnie do ruchu wskazówek zegara. Oblicz długość odcinka BB’.
Zad. 7*. (2 pkt) Przeciwprostokątna trójkąta prostokątnego ma długość 12 cm, a jeden z jego kątów ostrych ma miarę 30°. Oblicz długość środkowej poprowadzonej z wierzchołka tego kąta. Środkowa to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku.
odpowiedzi
grupa A
1. 60 cm2
2. a) 4√2, 4√2, b) 10, 5√3
3. a) z=5 lub z=√7, b) √7<z<5, c) 1<z<√7 lub 5<z<7
4. przekątna = √241 cm, pole = 60 cm2
5. 8√10 cm
6. 2√5
7. 3√7 cm
grupa B
1. 48 cm2
2. a) 3√2, 3√2, b) 4, 4√3
3. a) z=10 lub z=2√7, b) 2√7<z<10, c) 2<z<2√7 lub 10<z<14
4. obwód = 64 cm, pole = 240 cm2
5. 8√5 cm
6. 2√5
7. 3√13 cm
kryteria oceniania
1. 1 pkt za zastosowanie tw. Pitagorasa do odpowiedniego trójkąta, 1 pkt za obliczenie wysokości, 1 pkt za odpowiedź
2. a) - b) 1 pkt za każdy bok
3. a) - c) po 1 punkcie za każdą pełną odpowiedź
4. 1 pkt za długość ramienia, 1 pkt za wysokość trapezu, 1 pkt za pole, 1 pkt za przekątną/obwód
5. 1 pkt za wyrażenie pola rombu za pomocą długości jednej przekątnej, 1 pkt za zastosowanie tw. Pitagorasa do wyznaczenia długości boku, 1 pkt za obwód
6. 1 pkt za wyznaczenie współrzędnych punktu B', 1 pkt za długość odcinka
7. 1 pkt za rysunek z zaznaczonymi kątami i długościami odcinków, 1 pkt za zastosowanie tw. Pitagorasa i wynik
