Sołectwo to jednostka pomocnicza gminy, powoływana uchwałą rady tej gminy (czyli wszystkich radnych wybranych w powszechnych wyborach do rad gmin). Najczęściej sołectwo obejmuje obszar wsi, ale może się zdarzyć, że w jednej wsi jest kilka sołectw, albo że jedno sołectwo obejmuje kilka wsi. Sołectwo może znajdować się też na obszarze miasta, chociaż w większych miastach jednostkami pomocniczymi gminy są zazwyczaj osiedla i dzielnice. Sołectwa mogą istnieć tylko małych miastach, bo te, jeśli mają do 5 tysięcy mieszkańców, albo jeśli mają poniżej 20 tysięcy mieszkańców, ale nie mają szkoły średniej kończącej się maturą, są zaliczane do tzw. obszarów wiejskich, mimo że formalnie posiadają prawa miejskie.
W Polsce jest około 40,5 tysiąca sołectw na około 50,5 tysiąca miejscowości wiejskich (w tej liczbie jest 43 tysiące wsi). Na czele sołectwa stoi sołtys. Jest on organem władzy wykonawczej, a organem władzy ustawodawczej w sołectwie jest zebranie wiejskie.
Od kilku lat rady gmin mogą tworzyć fundusze sołeckie, czyli podejmować uchwały o wydzieleniu określonych środków pieniężnych z budżetu gminy i oddaniu ich do dyspozycji danego sołectwa. Zebranie wiejskie może przeznaczyć pieniądze z tego funduszu na dowolne cele zgodne z zadaniami własnymi gminy, do których należą np. remonty dróg gminnych (nie będących drogami krajowymi lub wojewódzkimi), budowa infrastruktury wodociągowej i kanalizacyjnej, wydatki na kulturę, oświatę, sport, ochronę zdrowia czy na promocję. Ustawa o funduszu sołeckim podaje wzór, który określa wysokość funduszu sołeckiego F = (2+Lm/100)·Kb, gdzie
Lm - liczba mieszkańców sołectwa na dzień 30 VI roku poprzedzającego dany rok budżetowy
Kb - kwota bazowa obliczana jako iloraz dochodów bieżących gminy za rok poprzedzający dany rok budżetowy o dwa lata i liczby mieszkańców gminy na dzień 31 XII roku poprzedzającego dany rok budżetowy o dwa lata.
Na wielkość F nałożone jest ograniczenie górne w wysokości 10·Kb, co oznacza, że fundusz sołecki nie może być dowolnie duży.
Aby zachęcić gminy do tworzenia funduszy sołeckich, wprowadzono zasadę, że otrzymują one z budżetu centralnego zwrot wydatków poniesionych w ramach funduszy sołeckich w wysokości 20%, 30% lub 40% tych wydatków. Wysokość tego zwrotu jest uzależniona od kwoty bazowej wyliczonej dla danej gminy.
Przykład 1. Oblicz wysokość funduszu sołeckiego w 2015 roku dla sołectwa Stawiska, w którym 30 VI 2014 roku mieszkało 300 osób. Dochody bieżące gminy, na terenie której leżą Stawiska, w 2013 roku wyniosły 10 mln zł, a liczba mieszkańców tej gminy 31 XII 2013 roku wynosiła 2000.
Rozwiązanie. Wysokość funduszu sołeckiego Stawisk wynosi F = (2+300/100)·10000000/2000 = 25000 zł.
Zadanie 1. Oblicz wysokość funduszu sołeckiego Wielkiej Wsi, w której od wielu lat mieszka stale tych samych 13 mieszkańców. Kwota bazowa gminy, na terenie której leży Wielka Wieś, wynosi 2 500 zł.
Zadanie 2. Dochody gminy Dudniewo za rok 2012 wynosiły 13,5 mln zł, a liczba mieszkańców 31 grudnia 2012 roku wyniosła 6645 osób. Jaka jest kwota bazowa dla Dudniewa w 2014 roku?
Zadanie 3. Oblicz wysokość funduszu sołeckiego w 2015 roku dla sołectwa Sroki zamieszkałego 30 VI 2014 roku przez 895 osób. Dochody gminy, w której leżą Sroki, w 2013 roku wynosiły 18,6 mln zł, a liczba jej mieszkańców na dzień 31 XII 2013 roku wynosiła 4320 osób.
Zadanie 1. Oblicz wysokość funduszu sołeckiego w 2015 roku dla sołectwa Sroki Małe, zamieszkałego 30 VI 2014 roku przez 1995 osób. Dochody gminy, w której leżą Sroki Małe, w 2013 roku wyniosły 19,6 mln zł, a liczba mieszkańców tej gminy 31 XII 2013 roku wynosiła 6320 osób.
Zadanie 2. Od ilu mieszkańców sołectwa wysokość funduszu sołeckiego nie ulega już zwiększeniu?
Zadanie 3. Jaką funkcję we wzorze na wysokość funduszu sołeckiego pełni liczba 2?
Zadanie 1. Ilu mieszkańców miało sołectwo Sroki Średnie w dniu 30 VI 2014 roku, jeśli 31 XII 2013 roku liczba mieszkańców gminy, w której leżą Sroki Średnie, wynosiła 4900 osób, dochody tej gminy w 2013 roku wyniosły 20,58 mln zł, a fundusz sołecki Srok Średnich w 2015 roku opiewał na 42 000 zł?
Zadanie 2. Sporządź wykres przedstawiający wysokość funduszu sołeckiego w zależności od liczby mieszkańców sołectwa przy ustalonej kwocie bazowej.
Zadanie 3. Oblicz wysokość funduszu sołeckiego w 2015 roku w Zagórzu zamieszkałym 30 VI 2014 roku przez 1190 osób. Dochody gminy, w której leży Zagórze, w 2013 roku wynosiły 38 mln zł, a liczba mieszkańców tej gminy 31 XII 2013 wynosiła 9540 osób.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Alicja Koźlik SP 44 Wrocław, Jakub Ptak SP 64 Wrocław, Bartosz Szczerba SP 35 Szczecin, Wojciech Szwarczyński SP Kowalowa i Kacper Woszczek SP Mieroszów;
- 2 pkt. - Weronika Szemplińska SP Drohiczyn.
Po dziewięciu miesiącach w czołówce Ligi z Matematyki Finansowej dla Szkół Podstawowych znaleźli się (w nawiasach podajemy liczby uzyskanych punktów na 27 możliwych):
I m. - Jakub Ptak (26)
II m. - Bartosz Szczerba (25 pkt)
III m. - Wojciech Szwarczyński (24)
IV m. - Alicja Koźlik (22,5)
V m. - Kacper Woszczek (20,5).
Gratulujemy!
W tym miesiącu punkty zdobyli:
- 2,5 pkt. - Joanna Lisiowska KZE Warszawa.
Po dziewięciu miesiącach w czołówce Ligi z Matematyki Finansowej dla Gimnazjów znaleźli się (w nawiasach podajemy liczby uzyskanych punktów na 27 możliwych):
I m. - Joanna Lisiowska (24,5)
II m. - Karol Szempliński, GM Salomon Drohiczyn (15,5)
III m. - Jakub Czerniak, GM 5 Opole (6,5).
Gratulujemy!
W tym miesiącu punkty zdobyli:
- 3 pkt. - Tomasz Stempniak I LO Ostrów Wielkopolski;
- 2,5 pkt. - Daria Bumażnik II LO Jelenia Góra i Wojciech Wiśniewski I LO Giżycko;
- 1 pkt. - Adam Pięta LO Żary.
I m. - Tomasz Stempniak (25,5)
II m. - Daria Bumażnik (23,5)
III m. - Wojciech Wiśniewski (21,5)
IV m. - Samanta Walczak, II LO Wieluń (16,5)
V m. - Adam Pięta (15).
Gratulujemy!
Zad. 1. Wysokość funduszu sołeckiego Wielkiej Wsi wynosi F = (2+13/100)·2500 = 5 325 zł.
Zad. 2. Kwota bazowa Dudniewa to 13500000/6645 ≈ 2 031,60 zł.
Zad. 3. Wysokość funduszu sołeckiego Srok jest mniejszą z kwot 10·18600000/4320 ≈ 43 055,56 zł i (2+895/100)·18600000/4320 ≈ 47 145,83 zł, czyli wynosi 43 055,56 zł.
Zad. 1. Wysokość funduszu sołeckiego Srok Małych jest mniejszą z kwot 10·19600000/6320 ≈ 31 012,66 zł i (2+1995/100)·19600000/6320 ≈ 68 072,78 zł, czyli wynosi 31 012,66 zł.
Zad. 2. Aby odpowiedzieć na pytanie z zadania, należy rozwiązać nierówność F ≥ 10·Kb, która prowadzi do warunku Lm ≥ 800. Dla sołectw z liczbą mieszkańców co najmniej równą 800, wysokość funduszu sołeckiego jest stale równa 10·Kb.
Zad. 3. Liczba 2 sprawia, że sołectwa z małą liczbą mieszkańców dostają fundusz sołecki nie mniejszy niż 2·Kb. Jeśli we wzorze nie byłoby liczby 2, to małe sołectwa dostawałyby bardzo małe kwoty.
Zad. 1. Zauważmy, że Kb = 4 200 zł, czyli kwota bazowa jest 10 razy mniejsza od wysokości funduszu sołeckiego. Oznacza to, że liczba mieszkańców tego sołectwa wynosi co najmniej 800 (zobacz rozwiązanie zadania 2 dla GIM).
Zad. 2. Dla uproszczenia przyjmujemy, że kwota bazowa jest równa 1 zł.
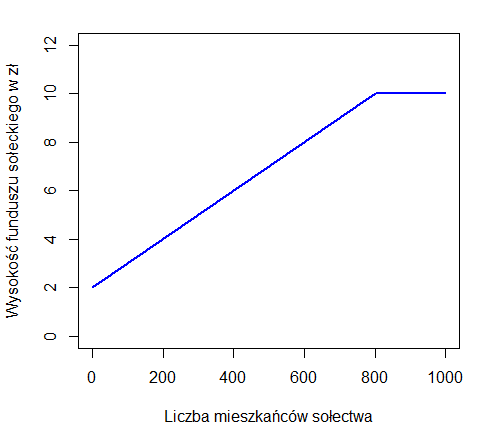
Zad. 3. Wysokość funduszu sołeckiego Zagórza jest mniejszą z kwot 10·38000000/9540 ≈ 39 832,29 zł i (2+1190/100)·38000000/9540 ≈ 55 366,88 zł, czyli wynosi 39 832,29 zł.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
