Zad. 1. Pewien wielokąt wypukły przecięto wzdłuż prostej na dwie części. Okazało się, że liczby wierzchołków tych części oraz początkowego wielokąta to trzy kolejne liczby naturalne. Ile wierzchołków miał początkowy wielokąt?
Zad. 2. Dla jakich wartości parametru a równanie (a2+1)(x2+y2) – 2(a+1)(x+y) + 2(1+2axy) = 0 ma dokładnie jeden pierwiastek?
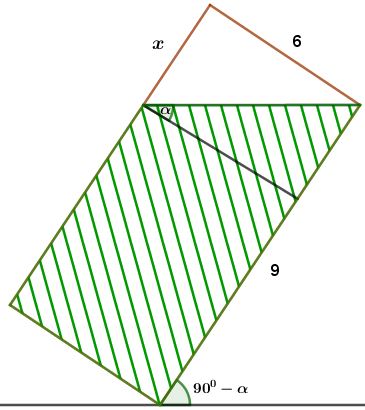
Zad. 3. Szklankę w kształcie walca o średnicy 6 cm i wysokości 9 cm napełniono wodą. Następnie przechylono ją tak, że 1/3 wody wylała się. Wyznacz miarę kąta, pod którym przechylono szklankę.
W grudniu punkty zdobyli:
- 3 pkt. – Jakub Dobrzański I LO Lubin, Julia Musiał II LO Tczew i Laura Stefanowska Katolickie LO Legnica;
- 2,5 pkt. – Łukasz Goliczewski LO Góra i Alex Kalinowski LO Góra;
- 2 pkt. – Piotr Zug I LO Olesno i Szymon Misiewicz CKZiU Strzelin;
- 1,5 pkt. – Michał Tokarski II LO Oleśnica, Mateusz Łakomiec XXVII LO Warszawa, Wiktoria Malinowska XXVII LO Warszawa,
- 1 pkt. – Adrian Szymański II LO Oleśnica, Mikołaj Dyblik VII LO Wrocław, Marcin Wiśniewski LO Ząbkowice Śląskie, Jakub Niedźwiedź XXVII LO Warszawa
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Niech n będzie liczbą wierzchołków danego wielokąta. Wtedy n–2 i n–1 to liczby wierzchołków wielokątów powstałych w wyniku przecięcia wielokąta wyjściowego.
I przypadek: prosta cięcia przechodzi przez dwa wierzchołki wielokąta
Wówczas suma liczb wierzchołków powstałych wielokątów jest o 2 większa od liczby wierzchołków wyjściowego wielokąta, czyli (n–2) + (n–1) = n+2, skąd n = 5.
II przypadek: prosta cięcia przechodzi przez wierzchołek wielokąta i jeden z boków
Wówczas suma liczb wierzchołków powstałych wielokątów jest o 3 większa od liczby wierzchołków wyjściowego wielokąta, czyli (n–2) + (n–1) = n+3, skąd n = 6.
III przypadek: prosta cięcia przechodzi przez dwa boki wielokąta
Wówczas (n–2) + (n–1) = n+4, skąd n = 7.
Ostatecznie wielokąt może mieć 5, 6 lub 7 wierzchołków.
Natomiast w przypadku czworokąta można zauważyć, że prosta przechodząca przez jego sąsiednie boki rozcina go na trójkąt i pięciokąt, zatem gdyby pominąć kolejność liczb sugerowaną w treści zadania, można by uznać, że n=4 także spełnia podane warunki.
Zad. 2. Przekształcając równanie równoważnie, otrzymujemy (a2x2+2axy+y2) + (a2y2+2axy+x2) – 2(ay+y) – 2(ay+x) + 2 = 0, skąd [(ax+y)2 – 2(ax+y) + 1] + [(ay+x)2 – 2(ay+x) + 1] = 0. Po dalszych przekształceniach otrzymujemy (ax+y–1)2 + (ay+x–1)2 = 0. Suma liczb nieujemnych jest zerem wtedy i tylko wtedy, gdy obie są zerami, czyli ax+y = 1 oraz x+ay = 1. Są to równania dwóch prostych: y = -ax +1 oraz y = -x/a + 1/a. Aby przecięły się w jednym punkcie, nie mogą być równoległe, czyli współczynniki przy x muszą być różne. Stąd a ≠ 1/a, czyli a ≠ 1 oraz a ≠ -1.
Zad. 3. Objętość szklanki V = π.32.9 = 81π. Objętość wylanej wody V1 jest równa połowie objętości walca o promieniu 3 i wysokości x (patrz rysunek), więc V1 = 1/2 π . 32 . x = 1/3V = 27π. Stąd x=6, czyli przekrój osiowy tego walca jest kwadratem, a zatem α = 45°.








Uwaga do rozwiązania zadania 1
Jeżeli czworokąt przetniemy prostą przechodzącą przez dwa sąsiednie boki to otrzymamy wielokąty które mają 3 i 5 wierzchołków, zatem otrzymujemy ciąg 3, 4, 5. W treści zadania nie ustalono kolejności występowania liczb wierzchołków, zatem poprawnym rozwiązaniem jest również n = 4.