Zad. 1. Iloczyn trzech liczb pierwszych równa się pięciokrotności ich sumy. Jakie to liczby?
Zad. 2. Trzyelementowe ciągi o wyrazach dodatnich - arytmetyczny i geometryczny - mają jednakowe pierwsze i ostatnie wyrazy. Który z nich ma większą sumę?
Zad. 3. Oblicz objętość równoległościanu, którego wszystkie ściany są rombami o boku długości a i kącie ostrym α.
W tym miesiącu punkty zdobyli:
- 3 - Kamila Bojar ZSP Szprotawa, Konrad Bratek I LO Lwówek Śląski, Bartosz Czyżewski I LO Jelenia Góra, Dawid Hanrahan I LO Brzeg, Dariusz Jajeśniak II LO Kraków, Piotr Jażdżewski I LO Oleśnica, Michał Kępiński SLO Żary, Alina Langa I LO Oleśnica, Błażej Mrzygłód Technikum nr 5 Opole, Николай Шамаев 131 Szkoła Ogólnokształcąca Charków (Ukraina), Tomasz Stempniak I LO Ostrów Wielkopolski i Wojciech Wiśniewski I LO Giżycko;
- 2,5 - Karol Kowalski I LO Kraków;
- 2 - Krzysztof Bednarek III LO Wrocław, Kamil Demczyszyn Lotnicze zakłady Naukowe Wrocław, Mieszko Gałat I LO Bydgoszcz, Szymon Meyer II LO Opole, Mateusz Rzepecki III LO
Wrocław, Maksymilian Szcześniak LO Płock i Agata Zielazna III LO Ostrów Wielkopolski; - 1,5 - Rafał Pych LO Leżajsk;
- 1 - Elżbieta Gontarz I LO Oleśnica, Beata Janiak III LO Opole, Weronika Szatkowska I LO Oleśnica i Kinga Wróblewska VIII LO Wrocław.
Pozostałym uczestnikom nie przyznano punktów.
Po trzech miesiącach Ligi Zadaniowej z wynikiem 9 pkt. (na 9 możliwych) prowadzą: Bartosz Czyżewski, Dawid Hanrahan, Dariusz Jajeśniak, Николай Шамаев, Tomasz Stempniak i Wojciech Wiśniewski, drugie miejsce z wynikiem 8 pkt. zajmują: Michał Kępiński, Alina Langa i Szymon Meyer, a trzecie miejsce z wynikiem 7 pkt. zajmują: Konrad Bratek, Błażej Mrzygłód i Mateusz Rzepecki. Gratulujemy!
Zad. 1. Niech x, y i z będą szukanymi liczbami, wtedy xyz = 5(x+y+z). Ponieważ jedyną liczbą pierwszą podzielną przez 5 jest właśnie 5, to jedna z szukanych liczb jest równa 5. Stąd dostajemy równanie yz = 5+y+z. Przekształcając je, otrzymujemy (y–1)(z–1) = 6. Oba czynniki muszą być dzielnikami szóstki, czyli należeć do zbioru {±1, ±2, ±3, ±6}, ale jednocześnie liczby y i z muszą być pierwsze, czyli mogą należeć do zbioru {2, 3, 7}. Dla y=2, z=7 i symetrycznie dla y=7, z=2, a dla y=3, z nie jest pierwsze. Ostatecznie szukane liczby pierwsze to 2, 5 i 7.
Zad. 2. Oznaczmy wyrazy ciągu arytmetycznego przez x, a i y, a wyrazy ciągu geometrycznego przez x, g i y. Z własności ciągów wiemy, że a = (x+y)/2 oraz g = √xy. Średnia arytmetyczna jest zawsze większa lub równa średniej geometrycznej, bo gdyby było przeciwnie, otrzymalibyśmy sprzeczność, bowiem z faktu (x+y)/2 < √xy wynika, że x+y < 2√xy i dalej x2+y2<4xy, czyli (x–y)2<0. Zatem większą sumę ma ciąg arytmetyczny poza przypadkiem gdy x=y (ciąg arytmetyczny ma różnicę 0, a geometryczny iloraz 1). Wówczas sumy są równe.
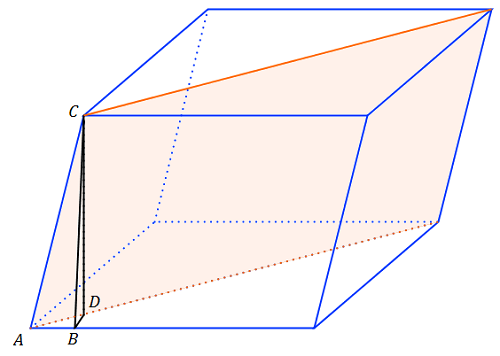
Zad. 3. Pole ściany równoległościanu wynosi a2sinα. Musimy obliczyć wysokość tej bryły. Niech CB jest wysokością ściany, a CD wysokością równoległościanu. Z trójkąta prostokątnego ABC wnioskujemy, że |AB| = |AC|cosα = acosα. Kąt DAB jest połową kąta CAB, bo przekątne rombu dzielą jego kąt na połowy. Trójkąt DAB jest prostokątny, bo to, że proste są w przestrzeni prostopadłe (w tym przypadku AB i CB) jest równoważne temu, że pierwsza z nich jest prostopadła do rzutu drugiej na płaszczyznę zawierającą tę pierwszą prostą, czyli prosta AB jest prostopadła do BD, która jest rzutem CB na płaszczyznę ABD. Zatem z trójkąta prostokątnego ABD wnioskujemy, że |AD|= |AB|/cos(α/2) = acosα/cos(α/2). Z twierdzenia Pitagorasa dla trójkąta prostokątnego ACD mamy |CD|2 = |AC|2–|AD|2 = a2 – (acosα/cos(α/2))2. Ostatecznie objętość równoległościanu wynosi[TEX]a^2\sin\alpha\sqrt{a^2-(\frac{a\cos\alpha}{\cos(\alpha/2)})^2}=a^3\sin\alpha\sqrt{1-(\frac{\cos\alpha}{\cos(\alpha/2)})^2}.[/TEX]Korzystając z tożsamości (dla kąta ostrego) [tex]\cos\frac{\alpha}{2}=\sqrt{\frac{1+\cos\alpha}{2}}[/tex], możemy uprościć wynik do postaci [TEX]a^3\sin\alpha\sqrt{1-\frac{2{\cos}^2\alpha}{1+\cos\alpha}}.[/TEX]
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
