Zad. 1. Znajdź wszystkie funkcje f(x) spełniające równanie [tex]\ 3f(x)+f\left(\frac{1}{x}\right)=x^2[/tex] , dla x≠0.
Zad. 2. Liczba 220 jest sumą ilorazu, iloczynu, różnicy i sumy dwóch liczb całkowitych. Jakie to liczby?
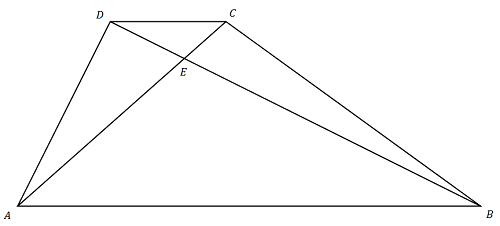
Zad. 3. Oblicz pole trapezu, znając pola dwóch trójkątów opartych na podstawach trapezu i o wspólnym wierzchołku w punkcie przecięcia przekątnych trapezu.
W tym miesiącu punkty zdobyli:
- 3 - Kamila Bojar ZSP Szprotawa, Bartosz Czyżewski I LO Jelenia Góra, Szymon Meyer II
LO Opole, Николай Шамаев 131 Szkoła Ogólnokształcąca Charków (Ukraina) i Tomasz Stempniak I LO Ostrów Wielkopolski; - 2,5 - Kamil Demczyszyn Lotnicze Zakłady Naukowe Wrocław, Dawid Hanrahan I LO Brzeg, Karol Kowalski I LO Kraków, Alina Langa I LO Oleśnica i Wojciech Wiśniewski I LO Giżycko;
- 2 - Błażej Mrzygłód Technikum nr 5 Opole;
- 1,5 - Krzysztof Bednarek III LO Wrocław, Konrad Bratek I LO Lwówek Śląski, Beata Janiak III LO Opole, Piotr Jażdżewski I LO Oleśnica i Michał Kępiński Społeczne LO Żary;
- 0,5 - Elżbieta Gontarz I LO Oleśnica, Kinga Wróblewska VIII LO Wrocław i Agata Zielazna III LO Ostrów Wielkopolski.
Pozostałym uczestnikom nie przyznano punktów.
Po czterech miesiącach Ligi Zadaniowej z wynikiem 12 pkt. (na 12 możliwych) prowadzą: Bartosz Czyżewski, Николай Шамаев i Tomasz Stempniak, drugie miejsce z wynikiem 11,5 pkt. zajmują: Dawid Hanrahan i Wojciech Wiśniewski, a trzecie miejsce z wynikiem 11 pkt. zajmuje Szymon Meyer. Gratulujemy!
Zad. 1. Podstawiając w miejsce argumentu wyrażenie 1/x, dostajemy równanie 3 f (1/x) + f (x) = x-2, które razem z równaniem 3 f (x) + f (1/x) = x2 tworzy układ równań. Mnożąc drugie równanie stronami przez 3 i odejmując od niego pierwsze równanie, otrzymujemy f (x) = (3x4–1)/8x2.
Trzeba jeszcze sprawdzić, że ta funkcja rzeczywiście spełnia warunki zadania (bo dodawanie równań stronami nie jest przejściem równoważnym).
Zad. 2. Oznaczmy szukane liczby przez a i b. Wiemy, że zachodzi 220 = a/b + a·b + a–b + a+b, co po uproszczeniu daje 220 = a/b + a·b + 2a = a/b(b+1)2. Aby równość zachodziła, a/b musi być liczbą całkowitą, czyli b musi być dzielnikiem a. Rozkład liczby 220 na czynniki pierwsze to 22·5·11, w którym można też dopisać dowolną potęgę liczby 1. Jedynymi kwadratami które dzielą 220 są 1 i 4, stąd b wynosi 1, -3 lub -2. Zatem szukanymi liczbami mogą być pary (55, 1), (-165, -3) lub (-440, -2).
Zad. 3. Ponieważ trójkąty CDE i BCE mają wspólną wysokość opuszczoną na DB, stosunek ich pól jest równy stosunkowi długości podstaw, czyli PΔBCE / PΔCDE = |EB|/|DE|. Trójkąty ABE i CDE są podobne (z cechy kkk), więc stosunek ich pól jest kwadratem skali podobieństwa, czyli √(PΔABE/PΔCDE) = |EB|/|DE|. Przyrównując te dwa wyrażenia, dostajemy PΔBCE = √(PΔABE·PΔCDE). Tyle samo wynosi pole trójkąta ADE (trójkąty ABC i ABD mają równe pola, a trójkąty BCE i ADE powstają z nich przez odjęcie trójkąta ABE). Pole trapezu jest sumą pól czterech trójkątów i wynosi
PΔABE + PΔCDE + PΔBCE + PΔADE = PΔABE + PΔCDE + 2√(PΔABE·PΔCDE) = (√PΔABE+√PΔCDE)2.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
