grudzień 2015

Zad. 1. Oto przykładowe 'pojęcia z nazwiskiem':

• okrąg: Apoloniusza, Eulera
• okręgi: Forda, Carlyle’a, Boromeuszy
• sfera: Aleksandera, Blocha, Hobermana, Riemanna
• sfery: Dandelina
• trójkąt: Pascala, Sierpińskiego, Releaux
• prosta: Eulera, Simsona
• krzywa: Gaussa, Peana, Hilberta, Jordana
• liczba: Nepera, Archimedesa
• liczby: Archimedesa, Catalana, Fermata, Fibonacciego, Mersenne'a 
• stała: Eulera, Chinczyna, Sierpińskiego
• wzór: Eulera, Herona, Picka
• wzory: Viete'a, Cramera, Cardana
• reguła: de L'Hospitala, Guldina, Cavaleriego, Sarrusa
• wielomian: Lagrange'a
• równanie: Cauchy'ego, Pella
• funkcja: Eulera, Dirichleta, Riemanna
• całka: Riemanna, Archimedesa
• miara: Jordana, Lebesque'a, Haara
• metryka: Minkowskiego, Czebyszewa, Hausdorffa
• paradoks: Russela, Bertranda, Zenona z Elei

Nie uznawaliśmy niektórych odpowiedzi, np.: metryka Euklidesa, trójkąt Pitagorasa, równanie Diofantosa (nie istnieją, zapewne chodziło o: metrykę euklidesową, trójkę pitagorejską, równanie diofantyczne), paradoks Achillesa (to jest jeden z paradoksów Zenona z Elei, jego poprawna nazwa to paradoks Achillesa i żółwia i to nie jest 'pojęcie z nazwiskiem'), sfera Dysona lub Bernala, stała Plancka lub Avogadra (nie są pojęciami matematycznymi). Nie odejmowaliśmy punktów za błędy w pisowni nazwisk, o ile były incydentalne.

Zad. 2. Ekierka Binga to przyrząd służący do przybliżonego rozwiązania problemu kwadratury koła, czyli konstrukcji kwadratu o polu równym polu danego koła. Metodę tę opisał w 1836 roku rosyjski inżynier Bing.

Niech x oznacza szukaną długość boku kwadratu o polu takim, jak pole koła o danym promieniu r. Kąt ACB jest wpisany i oparty na średnicy, więc jest prosty. Pole kwadratu o boku AC wynosi x² = (2r·cosα)², co ma być równe πr². Obliczamy stąd cosα = ¹/₂·√π. Widać, że kąt α nie zależy od r, jest więc ten sam dla każdego koła i wynosi ok. 27°35'49,6".

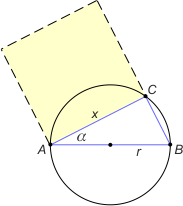
Wystarczy zatem sporządzić ekierkę (trójkąt prostokątny) o kątach ostrych 27°36' i 62°24", położyć wierzchołek jej najmniejszego kąta na obwodzie koła, a przeciwprostokątną ułożyć wzdłuż średnicy. Wówczas cięciwa wyznaczona przez przyprostokątną przyległą do tego kąta, jest bokiem szukanego kwadratu. Ponieważ tg27°36' ≈ 0,523 = 131/250, w praktyce można wykonać ekierkę Binga, biorąc za długości jej przyprostokątnych 131 i 250.

Zadanie okazało się trudne. Poprawnej odpowiedzi udzielili jedynie: Krystyna Lisiowska, Bolesław Mokrski i Wojciech Tomiczek. Gratulujemy wiedzy i dociekliwości.

Zad. 3. Najstarsze naukowe koncepcje budowy układu słonecznego (nie pytaliśmy o koncepcje budowy całego wszechświata) pochodzą od astronomów babilońskich (-XIX wiek), według których Ziemia była nieruchomą półkulą przykrytą sferycznym kloszem sklepienia niebieskiego, po którym poruszały się Słońce, Księżyc i gwiazdy.  Niektórzy zawodnicy podawali więcej niż 4 koncepcje. Wymagaliśmy, aby wśród nich wymienione były następujące:

• Klaudiusz Ptolemeusz (II wiek), teoria geocentryczna: nieruchoma Ziemia w centrum wszechświata, jednostajny ruch Słońca i Księżyca po okręgu, jednostajne ruchy planet po trajektoriach będących wynikiem złożenia ruchów po okręgach.
• Mikołaj Kopernik (XV/XVI wiek), teoria heliocentryczna: Słońce nieruchome w centrum wszechświata, jednostajne ruchy planet po trajektoriach będących wynikiem złożenia ruchów po okręgach (ale ich liczba była znacznie mniejsza niż w systemie ptolemejskim).
• Tycho Brahe (XVI wiek), teoria bicentryczna: wirująca Ziemia w centrum, wokół którego krążą jednostajnie po okręgach Słońce i Księżyc, planety zaś krążą po okręgach wokół Słońca.
• Johannes Kepler (XVI/XVII wiek), teoria helioacentryczna: ruch planet po elipsach, w których ognisku jest Słońce, ze zmiennymi prędkościami (stałe są prędkości polowe). Podwaliny teoretyczne tego modelu dał Izaak Newton (XVII wiek), formułując zasady dynamiki i prawo grawitacji, a jego potwierdzenie eksperymentalne przyniosły obserwacje aberracji światła przeprowadzone przez Jamesa Bradleya (XVIII wiek).

Uwaga! Jeśli coś porusza się wokół Ziemi, to zdecydowanie przez jedno 'i' - ten ortograficzny lapsus przydarzył się kilku osobom.