Zad. 1. W kwadracie o boku 3 zawiera się kwadrat o boku 2 i koło o promieniu 1. Oblicz największe i najmniejsze możliwe pole ich części wspólnej.
Zad. 2. Znajdź zbiory A, B i C, jeśli wiadomo, że:
$A \cup B= \langle 0,4 \rangle \setminus \{ 2 \}\ $ i $\ B \cup C= \{ 0 \} \cup \langle 1,4 \rangle$,
$A \cap B= \langle 1,3) \setminus \{ 2 \} \ $ i $\ B \cap C=(2,3 \rangle$ ,
$A \setminus C=(0,2) \ $ i $\ B \setminus A= \langle 3,4 \rangle$ .
Zad. 3. Okrąg o1 leży wewnątrz okręgu o2. Jaką figurę tworzą środki okręgów stycznych jednocześnie do o1 i o2?
Za rozwiązanie 3 zadań punkty zdobył tylko Damian Olczyk z I LO w Oleśnie.
Gratulujemy!
Najlepszym uczestnikiem od początku trwania Ligi jest również Damian Olczyk (19 pkt. na 21 możliwych).
Zad. 1. Największa możliwa część wspólna to całe koło, więc jej pole wynosi π. Aby część wspólna była najmniejsza, kwadrat i koło trzeba umieścić symetrycznie w przeciwległych rogach większego kwadratu, jak najdalej od siebie. Koło będzie wówczas styczne do dwóch jego boków, a mniejszy kwadrat może z wycinać ćwiartkę koła - gdy jego boki są równoległe do boków dużego kwadratu - albo pewien odcinek kołowy (część koła odciętą przez cięciwę) - gdy boki ma równoległe do przekątnych dużego kwadratu - patrz rys.
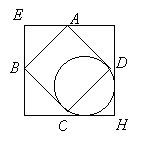
Odległość AB od E wynosi wówczas 1 (1/2 AB - z symetrii), więc CD jest odległe od H o 3√2-(1+2)=3(√2-1)<√2, więc ABCD wycina z koła więcej niż połowę (bo jego środek leży w odległości √2 od H). Zatem szukane najmniejsze pole to π/4.
Zad. 2. $ A = (A \cup B) \setminus (B \setminus A) = \langle 0,3) \setminus \{ 2 \}$ ,
$ B = (B \setminus A) \cup (A \cap B) = \langle 1,4 \rangle \setminus \{ 2 \}$,
$ C = (B \cup C) \setminus (B \setminus (B \cap C)) = \{ 0 \} \cup \langle 2,3 \rangle $.
Należy jeszcze sprawdzić, czy otrzymane zbiory spełniają warunki zadania. Tak jest!
Zad. 3. Wybierzmy dowolny z takich okręgów i oznaczmy jego środek przez S, a promień przez r. Środki i promienie okręgów danych w zadaniu oznaczmy odpowiednio przez S1, S2 i r1, r2. Mamy wówczas SS1+SS2= (r+r1)+(r2-r) = r1+r2 albo SS1+SS2= (r-r1)+(r2-r) = r2-r1, czyli w każdym z przypadków suma odległości S od S1 i S2 jest pewną stałą wielkością. Punkty S tworzą więc dwie elipsy (o ogniskach w S1 i S2), w szczególnym przypadku (przy jak położonych wyjściowych okręgach?) stające się okręgami.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
