Zad. 1. Zapisano wszystkie liczby naturalne, zaczynając od n, a kończąc na n2. Wszystkich tych liczb było 601. Ile wynosiło n?
Zad. 2. Ciuchcia w lunaparku porusza się ze stałą prędkością po zamkniętym torze o długości 60 m. Postanowiono zwiększyć prędkość kolejki o 0,4 km/h. Wojtek zauważył, że mimo to czas przejażdżki sie nie zmienił, za to kolejka wykonuje o jedno okrążenie więcej. Ile minut trwa przejażdżka?
Zad. 3. Martyna rozcięła kwadratową kartkę papieru na dwa jednakowe prostokąty. Każdy z nich złożyła tak, że otrzymała powierzchnie boczne dwóch różnych graniastosłupów prawidłowych czworokątnych. Suma objętości tych graniastosłupów wynosi 375 cm3. Ile jest równe pole kartki, którą Martyna miała na początku?
W kwietniu punkty zdobyli:
- 3 pkt. – Patryk Boruń SP 2 Wałbrzych, Adam Chowanek SP Mieroszów, Emilia Cichowska SP 14 Lubin, Wojciech Domin SP Pisarzowice, Zuzanna Dropia SP Świerże Górne, Michał Dźwigaj SP 1 Przemków, Paulina Hołodniuk SP 2 Wołów, Wiktoria Jaguszczak SP Grębocice, Zuzanna Lipka SP Jedlnia – Letnisko, Sandra Łuczak SP 107 Wrocław, Jakub Malicki SP Kobierzyce, Antoni Maracewicz SP Aslan Głogów, Paweł Michałowski PrSP 1 Białystok, Tymoteusz Noremberg SP 29 Wrocław, Julia Osowiec SP 3 Tarnowskie Góry, Michał Plata SP 2 Syców, Cezary Rębiś SP Jedlnia Letnisko, Karol Skowera SP 2 Wałbrzych, Tymosz Srokosz SP 52 Warszawa, Filip Timofiejczuk SP 3 Tarnowskie Góry, Michał Węgrzyn SP 9 Wrocław, Aleksandra Wiercińska SP Raszówka, Szymon Wróbel SSP Gliwice;
- 2,5 pkt. – Maja Muszyńska SP Jedlnia Letnisko;
- 2 pkt. – Lena Nowacka SP 28 Wałbrzych, Alicja Stachowska SP 28 Wałbrzych, Piotr Szymiec SP Pępowo.
Pozostali uczestnicy otrzymali poniżej 1 punktu
Zad. 1. Wszystkich wypisanych liczb było n2–(n–1) = n2–n+1 = 601, czyli n2–n = 600, a stąd n(n–1) = 600. Ponieważ n jest liczbą naturalną i 25.24 = 600, więc n=25.
Zad. 2. Oznaczmy przez t czas jednej przejażdżki w godzinach, a przez v - początkową prędkość kolejki w km/h. Długość jednego okrążenia wynosi 0,06 km. Porównując drogi, otrzymujemy równanie (v+0,4)t = xv+0,06t. Jedna przejażdżka kolejką trwa 6/40 godziny, czyli 9 minut.
Zad. 3. Oznaczmy przez a długość boku kwadratu. Podział kwadratu i zagięcia wyznaczają odcinki, których długość podana jest na rysunku poniżej.
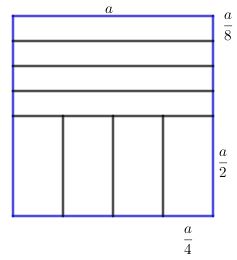
Objętości graniastosłupów wynoszą V1= (a/4)2·a/2 = a3/32 oraz V2= (a/8)2·a = a3/64. Skoro V1+V2=375, to a3=8000, skąd a=20. Pole kartki na początku wynosiło 400 cm2.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
