W tym miesiącu proponujemy zadania primaaprilisowe. Gdzie tkwi błąd? A może go nie ma?
Zad. 1.
a+b = c /·2
2a+2b = 2c /·2
4a+4b = 4c / (4 = 2+2)
4a+4b = 2c+2c / z II linii
4a+4b = 2a+2b+2c / –4c
4a+4b–4c = 2a+2b+2c–4c / (-2=2-4)
4a+4b–4c = 2a+2b–2c / wyciągamy wspólny czynnik przed nawias
4(a+b–c) = 2(a+b–c) / :(a+b–c)
4 = 2
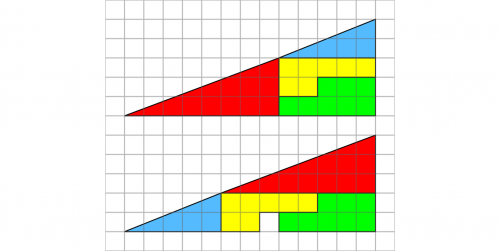
Zad. 2. Gdzie podział się brakujący kwadrat?
Zad. 3.
1 zł = 100 gr = 10 gr · 10 gr = 0,1 zł · 0,1 zł = 0,01 zł = 1 gr
W kwietniu punkty zdobyli:
- 3 pkt. – Maria Bochenek SP Mieroszów, Ryszard Bogacz SP Smolec, Natalia Czurejno SP Wykroty, Wiktor Kuczaj SP 7 Nowa Ruda, Joanna Nowakowska SP 3 Głogów, Wiktoria Pietrzak SP 3 Głogów, Maciej Pisowacki SP Mieroszów, Oliwia Raszewska SP 6 Boguszów-Gorce, Wiktor Szwarczyński SP Mieroszów, Kacper Wereszczyński PSP Mieroszów, Anastasiia Yakovleva SP 3 Mogilno;
- 2 pkt. – Kevin Charchut SP Iwierzyce, Mateusz Galik SP Arka Wrocław, Maciej Hryniewicz SP 9 Gliwice, Aleksander Masztalski SP 3 Mikołów, Zofia Prygiel SP Jedlnia Letnisko, Oliwia Stańczyk SP Aslan w Głogów, Julia Kubeczko SP Studzienice, Ignacy Włodarski SP 36 Wrocław;
- 1 pkt. – Dominika Wojdacz SP 11 Inowrocław, Tomasz Zawadzki SP Wodzisław.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Z równania a+b=c wynika, że a+b-c=0, zatem wykonanie przedostatniego działania
4(a+b–c) = 2(a+b–c) / :(a+b–c) jest niemożliwe.
Zad. 2. Złożone figury nie są trójkątami, jedna jest czworokątem wklęsłym, a druga wypukłym, a stąd różnica pól wynosząca 1 jednostkę kwadratową. Po dorysowaniu linii łączących górny i lewy dolny wierzchołek, widzimy, że punkty A, B i C oraz D, E i F nie są współliniowe.
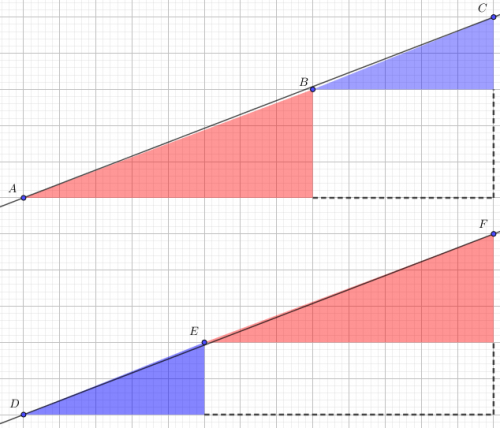
Zad. 3. 100 gr to 10 · 10 gr, a nie 10 gr · 10 gr.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
Wyniki
Czy mogą Państwo odpisywać na e-maile? Po zobaczeniu wyników córka sądzi, że odpowiedzi, które podała, są również zgodne z treścią zadań, a mimo to otrzymała mniejszą liczbę punktów. Z góry dziękuję.