Zad. 1. W poniedziałek pierwsza ciężarówka zrobiła 4 kursy, a druga 3. Razem wywiozły mniej niż 21 ton gruzu. Nazajutrz pierwsza ciężarówka zrobiła 7 kursów, druga 4 i razem wywiozły więcej niż 33 tony gruzu. Która z ciężarówek ma większą ładowność? Odpowiedź uzasadnij. Zakładamy, że ciężarówki były zawsze maksymalnie obciążone.
Zad. 2. Znajdź wszystkie pary liczb całkowitych spełniające równanie [tex] \frac{x}{x-y}=y[/tex].
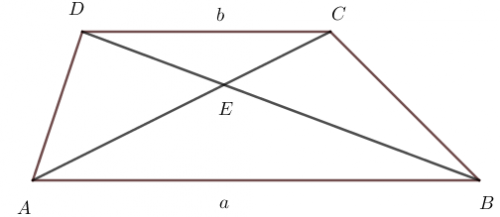
Zad. 3. Podstawy trapezu mają długości a i b. Oblicz stosunek pola trapezu do pola trójkąta utworzonego przez końce podstawy o długości b i punkt przecięcia przekątnych trapezu.
W kwietniu punkty zdobyli:
- 3 – Emilia Cichowska II LO Lubin, Wojciech Domin III LO Wrocław, Rafał Górzyński I LO Lubin, Wiktoria Prokop II LO Głogów, Wojciech Raszczuk I LO Bolesławiec, Michał Węgrzyn ALO PWr Wrocław;
- 2 – Karolina Szymandera I LO Inowrocław, Igor Wojtasik I LO Jelenia Góra.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Oznaczmy przez x udźwig pierwszej ciężarówki w tonach, a przez y - udźwig drugiej ciężarówki. Z treści zadania mamy 4x+3y < 21 i 7x+4y > 33, a stąd 44x+33y < 3·7·11 i 49x+28y > 3·11·7, więc 49x+28y > 3·11·7 > 44x+33y. Dalej 49x+28y > 44x+33y, czyli 5x–5y > 0, zatem x>y. Większą ładowność ma pierwsza ciężarówka.
Zad. 2. Załóżmy, że x≠y. Po przekształceniu równania [tex] \frac{x}{x-y}=y[/tex] otrzymujemy x(y–1) = y2. Dla y=1 jest to równanie sprzeczne. Po dalszym przekształceniu ostatniego równania otrzymamy [tex] x=\frac{y^2}{y-1} \Longleftrightarrow\frac{y^2-1+1}{y-1} \Longleftrightarrow x=y+1+\frac{1}{y-1}[/tex]. Ponieważ x ma być liczbą całkowitą, [tex] \frac{1}{y-1}[/tex] musi być liczbą całkowitą, czyli y–1 = -1 lub y–1 = 1. W pierwszym przypadku y=0 i wtedy x=0, co jest sprzeczne z warunkiem x≠y. W drugim przypadku y=2 i wtedy x=4. Jedyną parą liczb całkowitych spełniającą równanie jest (4, 2).
Zad. 3. Przyjmijmy oznaczenia jak na rysunku poniżej, a pole trójkąta DEC oznaczmy przez t. Zauważmy, że trójkąty ABE i DCE są podobne na podstawie cechy kkk (dlaczego?). Skala podobieństwa tych trójkątów wynosi k = a/b. Trójkąty EBC i DEC mają wspólną wysokość opuszczoną z wierzchołka C, więc stosunek ich pól jest równy stosunkowi długości podstaw, który wynosi |EB|:|ED| = k. Oznacza to, że PEBC = kt. Analogicznie uzasadniamy, że PAED = kt. Z podobieństwa trójkątów ABE i DCE wynika, że PABE = k2t (dlaczego?). Stąd
[tex] \frac{P_{ABCD}}{P_{DEC}}=\frac{k^2+2kt+t}{t}=k^2+2k+1=(k+1)^2=(\frac{a}{b}+1)^2 [/tex].
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
