Zad. 1. Ruchomy chodnik długości 100 m posuwa się z prędkością 2 m/s. Dwie osoby startują jednocześnie z przeciwnych końców tego chodnika z prędkością 2,5 m/s każda. W jakiej odległości od bliższego końca chodnika nastąpi spotkanie tych osób?
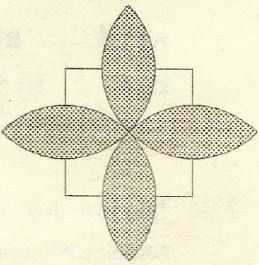
Zad. 2. Z każdego wierzchołka kwadratu o boku a zakreślono łuk okręgu przechodzącego przez środek kwadratu. Jakie jest pole powstałej w ten sposób rozety?
Zad. 3. Antek, Bartosz, Cezary i Damian chcą podzielić między siebie 10 jednakowych jabłek tak, aby każdy otrzymał co najmniej jedno. Na ile różnych sposobów mogą to zrobić?
W maju punkty zdobyli:
- 3 – Emilia Cichowska II LO Lubin, Wojciech Domin III LO Wrocław, Rafał Górzyński I LO Lubin, Wiktoria Prokop II LO Głogów, Wojciech Raszczuk I LO Bolesławiec, Karolina Szymandera I LO Inowrocław, Michał Węgrzyn ALO PWr Wrocław;
- 2 – Filip Kwidziński II LO Jelenia Góra, Igor Wojtasik I LO Jelenia Góra.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Osoba, która idzie zgodnie z kierunkiem ruchu chodnika, porusza się względem punktu wyjścia z prędkością 2+2,5 = 4,5 m/s. Osoba idąca w przeciwnym kierunku porusza się względem punktu startu z prędkością 2,5–2 = 0,5 m/s. W ciągu sekundy osoby zbliżają się o 5 m, a spotkają się po 100:5 = 20 sekundach. W tym czasie pierwsza z nich znajduje się w odległości 20.4,5 = 90 m od punktu wyjścia, zatem spotkanie nastąpi w odległości 10 m od bliższego końca chodnika.
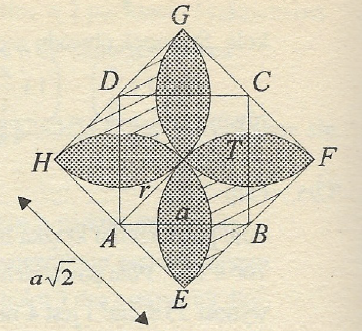
Zad. 2. Niech F oznacza pole rozety. Zauważmy, że jest ono równe różnicy pola kwadratu EFGH o boku a√2 i podwojeniu pola części zakreskowanej. Natomiast pole zakreskowane to różnica pola kwadratu EFGH i pola koła o promieniu r = a√2/2 (dlaczego?). Szukane pole wynosi [tex](a\sqrt{2})^2-2[(a\sqrt{2})^2-\pi(\frac{a\sqrt{2}}{2})^2]=a^2(\pi-2)[/tex].
Zad. 3. Zauważmy, że jeden z chłopców może otrzymać co najwyżej 7 jabłek. Dziesięć jabłek możemy rozdzielić na 9 sposobów: 7+1+1+1, 6+2+1+1, 5+3+1+1, 5+2+2+1, 4+4+1+1, 4+3+2+1, 4+2+2+2, 3+3+2+2, 1+3+3+3. W tych przypadkach uzyskamy następujące liczby możliwości podziału jabłek: 4, 4·3, 4·3, 4·3, 3·2, 4·3·2, 4, 3·2 i 4. Wszystkich sposobów podziału jest 3·4+3·(4·3)+2·(3·2)+4·3·2 = 84.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
