Zad. 1. Liczby x, y i z spełniają warunki: [tex]x=\sqrt{12-3\sqrt7}-\sqrt{12+3\sqrt7}[/tex], [tex]y=\sqrt{7-4\sqrt3}-\sqrt{7+4\sqrt3}[/tex], [tex]z=\sqrt{2+\sqrt3}-\sqrt{2-\sqrt3}[/tex]. Ile wynosi xyz?
Zad. 2. Funkcja f spełnia równanie (n−2019)·f(n) − f(2019−n) = 2019 dla każdej liczby całkowitej n. Ile wynosi wartość f(2019)?
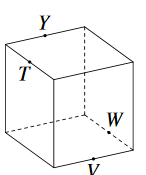
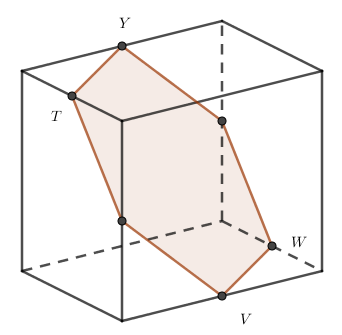
Zad. 3. Sześcian z rysunku ma krawędź długości 2. Bryłę przecina płaszczyzna przechodząca przez punkty Y, T i W (środki odpowiednich krawędzi). Jakie jest pole otrzymanego przekroju?
W listopadzie punkty zdobyli:
- 3 pkt. – Anna Cichowska II LO Lubin, Adam Chowanek III LO Wałbrzych, Wojciech Domin III LO Wrocław, Rafał Górzyński I LO Lubin, Dominik Pawelec II LO Dzierżoniów, Bartosz Kaczor I LO Głogów, Michał Plata III LO Wrocław, Cezary Rębiś ZSE Radom, Laura Stefanowska KLO Legnica, Igor Wojtun I LO Głogów;
- 2 pkt. – Martyna Babiak DLH Nysa, Karol Czub II LO Oleśnica, Filip Derejski I LO Kraków, Michał Dźwigaj LO Przemków, Kinga Kaczmarzyk NLF św. Jadwigi Wrocław, Mikołaj Popek VIII LO Poznań, Wojciech Szwarczyński II LO Wałbrzych, Igor Wojtasik I LO Jelenia Góra;
- 1 pkt. – Tomasz Chudziński DLH Nysa, Jakub Kutyła ZS Głogów.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Z treści zadania wynika, że x<0, y<0, z>0, skąd xyz>0. Podnieśmy liczby x, y i z do kwadratu.
[tex]x^2 =(\sqrt{12-3\sqrt{7}}-\sqrt{12+3\sqrt{7}})^2=12-3\sqrt{7}-2\sqrt{12-3\sqrt{7}}\cdot\sqrt{12+3\sqrt{7}}+12+3\sqrt{7}=24-2\sqrt{144-63}=24-18=6[/tex]
[tex]y^2 =(\sqrt{7-4\sqrt{3}}-\sqrt{7+4\sqrt{3}})^2=7-4\sqrt{3}-2\sqrt{7-4\sqrt{3}}\cdot\sqrt{7+4\sqrt{3}}+7+4\sqrt{3}=14-2\sqrt{49-48}=14-2=12[/tex]
[tex]z^2 =(\sqrt{2+\sqrt{3}}-\sqrt{2-\sqrt{3}})^2=2+\sqrt{3}-2\sqrt{2+\sqrt{3}}\cdot\sqrt{2-\sqrt{3}}+2-\sqrt{3}=4-2\sqrt{4-3}=4-2=2[/tex].
Zatem x2y2z2=144, czyli xyz=12.
Zad. 2. Dla n=0 otrzymujemy (-2019)·f(0)–f(2019) = 2019, skąd f(2019) = (-2019)·(1+f(0)), a dla n=2019 otrzymujemy 0·f(2019)–f(0) = 2019, skąd f(0)=-2019. Wobec tego f(2019) = (-2019)·(1–2019) = 4074342.
Zad. 3. Przekrój sześcianu płaszczyzną przechodzącą przez zaznaczone na rysunku środki krawędzi jest sześciokątem foremnym o boku długości √2 (połowa długości przekątnej ściany d=2√2). Pole tego sześciokąta wynosi 3√3.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
