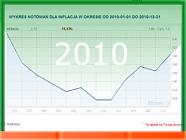
W czasie kryzysu ekonomicznego (na przykład takiego, z jakim obecnie zmaga się Grecja) wszyscy boją się wysokiej inflacji. Co to jest i dlaczego wysoka inflacja jest taka groźna?
Inflacja jest jedną z podstawowych miar ekonomicznych. Jest to średni wzrost cen towarów i usług w określonym czasie. Na skutek inflacji za tę samą kwotę możemy kupić mniej towarów i usług niż mogliśmy wcześniej. Jeśli wysokiej inflacji nie towarzyszy wzrost wynagrodzeń, ludzie ubożeją.
Przeciwieństwem inflacji jest deflacja. Ma miejsce wtedy, gdy towary i usługi tanieją i za tę samą kwotę możemy ich kupić więcej niż mogliśmy wcześniej.
Główny Urząd Statystyczny śledzi na bieżąco zmiany cen na polskim rynku i podaje (na podstawie określonego koszyka zawierającego ok. 100 produktów), jaki był w danym miesiącu, kwartale lub roku wskaźnik inflacji. Jest to wynik, który mówi, o ile procent w ciągu tego miesiąca, kwartału lub roku wzrosły średnio ceny towarów i usług.
Przykład 1. Greckie media podały, że w październiku 2011 roku wskaźnik inflacji wyniósł 5%. 1 X kilogram sera feta w sklepie osiedlowym w Salonikach kosztował 8 euro. Jakiej ceny za fetę możemy spodziewać się w tym sklepie 1 XI?
Rozwiązanie. Skoro inflacja w październiku wynosiła 5% (czyli 5/100), to kilogram sera feta najprawdopodobniej o tyle właśnie podrożeje, zatem jego cena w listopadzie wyniesie ok. (1+0,05)·8 = 8,40 euro.
Przykład 2. W innym sklepie w Salonikach cena czarnych oliwek z pestkami wzrosła w tym samym czasie z 3,00 do 3,30 euro. Właściciel tłumaczy niezadowolonym klientom, że to wszystko przez inflację. Czy mówi prawdę?
Rozwiązanie. Cena oliwek wzrosła o 0,30 euro, czyli o 1/10 ceny początkowej lub (inaczej mówiąc) o 10/100, czyli o 10%. To oznacza, że właściciel sklepu podniósł cenę oliwek o dwukrotnie więcej niż wynosił wskaźnik inflacji. W czasie kryzysu odpowiednie służby kontrolują i zwalczają takie nieuczciwe zawyżanie cen towarów pierwszej potrzeby.
Realna wartość nabywcza pieniądza określa, jak dużo jakiegoś towaru możemy kupić za ustaloną kwotę. Wartość ta zmienia się z powodu inflacji i deflacji. Inflacja powoduje, że realna wartość pieniądza maleje.
Powiedzmy, że w styczniu guma do żucia kosztowała złotówkę. Za 100 zł mogliśmy więc kupić 100 opakowań tej gumy. Przy rocznej inflacji wynoszącej 6% w grudniu ta sama guma kosztuje już 1,06 zł i za 100 zł możemy kupić tylko 100/1,06 ≈ 94 opakowania. W styczniu wystarczyłoby nam na to 94 zł. Mówimy więc, że w ciągu roku realna wartość nabywcza 100 zł spadła do 94 zł lub (co na to samo wychodzi), że po roku realna wartość złotówki spadła do 94 groszy.
[koniec wykładu dla SP]
Przykład 3. W pewnym roku wskaźnik inflacji w Polsce wynosił 5%. W styczniu tego roku za 100 zł mogliśmy kupić 50 kartonów mleka. Cena mleka zmieniała się tak samo, jak wskaźnik inflacji. Ile mleka mogliśmy kupić za 100 zł pod koniec grudnia? Jaka była po roku realna wartość nabywcza złotówki?
Rozwiązanie. W styczniu karton mleka kosztował 100:50 = 2 zł. Na skutek inflacji po roku cena mleka wzrosła o 5%, czyli karton mleka kosztował w grudniu (1+0,05)·2 = 2,10 zł. Dlatego po roku za 100 zł mogliśmy kupić tylko 47 kartonów mleka (bo 100:2,1 ≈ 47,62). Wartość tego mleka na początku roku wynosiła 47,62·2 = 95,24 i taka jest po roku realna wartość nabywcza kwoty 100 zł. Zatem wartość złotówki spadła po roku do 95 groszy.
GUS oblicza również wskaźniki inflacji dla poszczególnych grup towarów i usług z koszyka, na przykład energii, paliw, warzyw lub pieczywa. Natomiast Narodowy Bank Polski z poszczególnych wskaźników podanych przez GUS oblicza i ogłasza, jaka była inflacja w Polsce w danym roku.
Przykład 4. Roczne wskaźniki inflacji w Polsce w latach kryzysu na przełomie lat 80. i 90. XX wieku wynosiły: w 1989 roku 639,6%, a w 1990 roku 249,3%. Oblicz, o ile procent wzrosły średnio ceny towarów i usług w Polsce w czasie tych dwóch lat.
Rozwiązanie. Towar, który na początku roku 1989 kosztował złotówkę, pod koniec tego samego roku kosztował 7, 40 zł, bo (1+6,396)·1 = 7,396 zł. Z kolei po upływie roku 1990 ten sam towar kosztował już 25,83 zł bo (1+2,493)·7,396 = 25,834228. Oznacza to, że cena towaru wzrosła o 25,83 - 1 = 24, 83 zł, czyli o 2483%.
Zadanie 1. W pewnym roku procentowy wzrost ceny chleba był w Polsce taki sam, jak wskaźnik inflacji. Ile wynosiła wtedy inflacja roczna, jeśli chleb kosztujący w styczniu 1,90 zł do grudnia podrożał o 38 gr?
Zadanie 2. Jeżeli roczny wskaźnik inflacji wynosi 5%, to jaką wartość nabywczą po roku ma odłożona w styczniu do skarbonki kwota 500 zł?
Zadanie 3. Przyjmijmy, że w tym roku zmiana ceny oleju napędowego wyznacza zmiany wskaźnika inflacji w Polsce. Ile powinien wynieść wskaźnik inflacji w grudniu, aby cena 100 litrów oleju w Sylwestra nie przekroczyła 54,59 zł, jeśli obecnie 100-litrowy bak autokaru można zatankować za 53 zł?
Zadanie 1. Roczny wskaźnik inflacji w Polsce wyniósł w 2010 roku 2,6%. W styczniu 2010 pensja pana Jana wynosiła 3000 zł, a w grudniu 3050 zł. Czy realna wartość zarobków pana Jana wzrosła, czy zmalała? O ile procent zmieniła się realna siła nabywcza jego zarobków?
Zadanie 2. Roczne wskaźniki inflacji w Polsce w latach 2001–2010 wynosiły odpowiednio: 3,6%, 0,8%, 1,7%, 4,4%, 0,7%, 1,4%, 4,0%, 3,3%, 3,5% i 2,6%. Oblicz, o ile procent wzrosły średnio ceny towarów i usług w Polsce w czasie tej dekady.
Zadanie 3. Jeśli wskaźnik inflacji w pewnym roku wynosi 2,5%, to jaka powinna być roczna stopa procentowa dla lokat bankowych, aby z 8000 zł oszczędności włożonych na lokatę 1 stycznia uzyskać 31 XII odsetki o realnej wartości nabywczej 250 zł?
Zadanie 1. W firmie AQQ pracują dwaj informatycy: Adam i Zenon. Adam zarabiał 3200 zł a Zenon 4000 zł miesięcznie. Po roku, w którym wskaźnik inflacji wyniósł 3%, obaj dostali podwyżkę w wysokości 100 zł. Czy realna wartość nabywcza ich pensji wzrosła czy zmalała? Ile powinna wynosić podwyżka dla każdego z nich, aby realna wartość nabywcza ich pensji nie uległa zmianie?
Zadanie 2. Roczne wskaźniki inflacji w Polsce w latach 1991–1999 wynosiły odpowiednio: 60,4%, 44,3%, 37,6%, 29,5%, 21,6%, 18,5%, 13,2%, 8,6% i 9,8%. Oblicz, jaki był wskaźnik inflacji w 2000 roku jeśli inflacja w całej dekadzie 1991-2000 wyniosła 770,40%.
Zadanie 3. Jeśli wskaźnik inflacji w pewnym roku wynosi 2,5%, to jaka powinna być roczna stopa procentowa dla lokat bankowych, aby oszczędności nie straciły po roku na wartości? A jaka, aby zysk z lokaty o dwa punkty procentowe przewyższył wskaźnik inflacji?
W tym miesiącu 3 punkty zdobyli: Adam Gawlik SP 28 Wałbrzych, Anna Górska SP 2 Olesno, Joanna Lisiowska KSP Warszawa, Patrycja Łukasik SP w Mieroszów,
Aleksandra Piasecka KSP Oleśnica, Mateusz Rzepecki SP 91 Wrocław, Andrzej Turko SP Optimum Wrocław.
2,5 pkt. otrzymała Karolina Litwin SP Mieroszów.
Po 2 pkt. otrzymali: Alicja Baranowska SP 28 Wałbrzych, Dominik Bartuś SP 5 Żory, Aleksander Cząstkiewicz-Trawiński SP 14 Głogów, Dominik Frankowski SP Radwanice, Bartosz Mękarski SP Ciechów, Marek Mieniek SP 4 Bolesławiec, Wiktoria Płoneczka SP 5 ???.
1 pkt. uzyskała Barbara Kucaba SP Kobierzyna.
Pozostałym uczestnikom punktów w tym miesiącu nie przyznano.
Po dwóch miesiącach Ligi z wynikiem 6 pkt. prowadzą: Adam Gawlik SP 28 Wałbrzych, Anna Górska SP 2 Olesno, Joanna Lisiowska KSP Warszawa i Andrzej Turko SP Optimum Wrocław.
W tym miesiącu 3 punkty zdobyli: Krzysztof Bednarek GM 13 Wrocław, Daria Bumażnik GM 1 Jelenia Góra, Wojciech Górski GM 2 Olesno, Barbara Piasecka GM 3 Oleśnica.
2,75 pkt. uzyskała Izabela Domaracka GM 2 Wołów.
Po 2,5 pkt. uzyskali: Liwia Ćwiek GM 2 Złotoryja, Mieszko Gałat GM 50 Bydgoszcz, Anna Łeń GM 1 Łódź.
Po 2 pkt. uzyskali: Marta Przybyła GM 25 Wrocław, Bartosz Sójka GM 1 Jelenia Góra.
1,5 pkt. uzyskał Tomasz Zel GM Ruszów.
Po 0,5 pkt. uzyskali: Agnieszka Czekalska i Paulina Dudas GM Ruszów.
Pozostałym uczestnikom nie przyznano w tym miesiącu punktów.
Po dwóch miesiącach Ligi z wynikiem 6 pkt. prowadzą: Krzysztof Bednarek GM 13 Wrocław, Daria Bumażnik GM 1 Jelenia Góra, Wojciech Górski GM 2 Olesno i Barbara Piasecka GM 3 Oleśnica.
W tym miesiącu 3 punkty zdobyli: Mikołaj Andruniow XIV LO Wrocław, Aleksandra Pawłowska XIV LO Wrocław, Bartłomiej Polcyn I LO Inowrocław, Maciej Pomykała LA Toruń, Daria Sobieraj II LO Będzin, Disa Witkowska XIV LO Wrocław.
2,75 pkt. zdobył Jakub Sobyra I LO Tarnów.
Po 2,5 pkt. zdobyli: Karol Łukasik XIV LO Wrocław i Krzysztof Sadurski II LO Jelenia Góra.
2,25 pkt. zdobył Paweł Samoraj I LO Olsztyn.
Po 2 pkt. zdobyli: Artur Bogdan ???, Jagoda Janik XIV LO Wrocław, Jan Rostek XIV LO Wrocław.
Po 1,5 pkt. zdobyli: Adam Balawender ZSO Strzegom, Aleksandra Petrykiewicz XIV LO Wrocław, Ewa Piankowska XIV LO Wrocław, Tomasz Skalski III LO Wrocław.
1 pkt. zdobyła Marta Janik XIV LO Wrocław.
Po 0,5 pkt. zdobyli: Anna Budek II LO Będzin, Patrycja Dzwonkowska XIV LO Wrocław, Magdalena Zielonka VII LO Wrocław.
Pozostali uczestnicy nie otrzymali w tym miesiącu punktów.
Po dwóch miesiącach Ligi z wynikiem 6 pkt. prowadzą: Bartłomiej Polcyn I LO Inowrocław i Maciej Pomykała LA Toruń .
Zad. 1. Inflacja roczna wyniosła 38/190 = 2/100, czyli inaczej mówiąc, 20%.
Zad. 2. Towar, który kosztował złotówkę, po roku kosztuje 1,05 zł, zatem po roku za 500 zł możemy kupić towar, który na początku roku kosztował 500:1,05 ≈ 476,19 zł i taką wartość nabywczą ma po roku kwota 500 zł.
Zad. 3. Różnica cen oleju na poczatku i końcu grudnia wynosi 54,59 - 53 = 1,59 zł. Ta różnica stanowi 1,59/53 = 3/100 ceny z początku miesiąca. Zatem jeśli wzrost ceny grudniowej nie przekroczy 3%, cena 100 litrów oleju w Sylwestra nie przekroczy 54,59 zł. Zatem wskaźnik inflacji w grudniu nie powinien przekroczyć 3%. Ceny w zadaniu zostały dobrane w taki sposób, aby łatwo można było wykonać na nich obliczenia. W rzeczywistości na naszych stacjach benzynowy ceny są około 10 razy wyższe.
Zad. 1. Gdyby zarobki pana Jana wzrosły o poziom inflacji, to zarabiałby on w grudniu 3000·1,026 = 3078 zł. Oznacza to, że realna wartość jego zarobków zmalała o 28 zł. Towar, który na początku roku kosztował złotówkę, w grudniu kosztuje 1,026 zł. Za swoją grudniową pensję pan Jan może kupić towar, który w styczniu kosztował 3050/1,026 ≈ 2972,71 zł. Zatem siła nabywcza jego zarobków zmalała o 27,29 zł, czyli o 27,29/3050 ≈ 0,9%.
Zad. 2. Towar, który na początku dekady kosztował złotówkę, po roku kosztował 1,036 zł, po dwóch latach 1,008·1,036 zł, po trzech 1,017·1,008·1,036 zł itd. aż po 10 latach kosztował 1,026 · 1,035 · 1,033 · 1,04 · 1,014 · 1,007 · 1,044 · 1,017 · 1,008 · 1,036 ≈ 1,29 zł. Podrożał o 29% i o tyle wzrosły średnio ceny towarów i usług w czasie dekady (obliczając dokładniej, o 29,16 %).
Zad. 3. Realna wartość nabywcza w wysokości 250 zł oznacza, że w grudniu możemy kupić towar, który kosztował 250 zł w styczniu. W grudniu potrzeba nam na to 250·1,025 = 256,25 zł i tyle właśnie odsetek chcemy uzyskać po roku z lokaty. Kwota ta stanowi 256,25/8000 ≈ 3,2/100 lokaty 8000 złotowej, zatem dostaniemy ją w formie odsetek, gdy roczna stopa procentowa dla lokat wyniesie 3,2 %.
Zad. 1. Realna wartość nabywcza pensji Adama zwiększyła się, a Zenona zmalała. Aby realna wartość nabywcza ich pensji nie uległa zmianie, za nowe pensje powinni móc kupić tyle samo towaru, co na początku roku. To znaczy, że Adam powinien móc kupić towar za 3200·1,03 = 3296 zł, a Zenon za 4000·1,03 =4120 zł. Adam powinien wiec dostać tylko 96 zł podwyżki, a Zenon aż 120 zł.
Zad. 2. Towar, który na początku roku 1991 kosztował 1 zł, na początki 1992 roku kosztował 1,604 zł, na początku 1993 roku 1,443·1,604 zł itd. aż na początku 2000 roku kosztował 1,098 · 1,086 · 1,132 · 1,185 · 1,216 · 1,295 · 1,376 · 1,443 · 1,604 ≈ 8,02 zł, czyli podrożał o 7,02 zł, wiec o 702% (dokładniej 702,21 %). Pod koniec roku 2000 wskaźnik inflacji za dekadę wynosił 770,40%, tzn. towar za 1 zł z 1991 roku kosztował 1+7,70 = 8,70 zł. W stosunku do roku 1999 podrożał o 0,68 zł, czyli o 0,68/8,02 ≈ 85/100. Zatem wskażnik inflacji w 2000 roku wyniósł około 8,5 %.
Zad. 3. Aby oszczędności nie straciły po roku na wartości, oprocentowanie musi być co najmniej równe wskaźnikowi inflacji. Aby zysk z lokaty wyniósł 4,5 % ulokowanej kwoty, oprocentowanie roczne lokat powinno wynieść 4,5 %.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
