Począwszy od tego odcinka rozwiązania zadań prosimy przesyłać na adres mejlowy yolande@poczta.fm (adres pocztowy pozostaje bez zmian).
Zad. 1. Rozwiąż w liczbach rzeczywistych równanie sinx = (cosx – [cosx])·[cosx], gdzie [a] oznacza część całkowitą liczby a.
Zad. 2. Wyznacz wszystkie pary liczb pierwszych p i q, dla których liczba pq + qp jest pierwsza.
Zad. 3. W trapezie równoramiennym przekątne o długości 12 cm przecinają się w punkcie S pod kątem 30°. Punkty K, L, M, N są środkami boków trapezu. Oblicz pole czworokąta KLMN.
W lutym punkty zdobyli:
- 3 - Bartosz Czyżewski I LO Jelenia Góra, Błażej Mrzygłód V Technikum Opole, Paweł Wesołowski II LO Końskie, Wojciech Wiśniewski I LO Giżycko i Konrad Bratek I LO Bolesławiec;
- 2,5 - Mateusz Kwieciński I LO Bolesławiec i Patryk Szlufik II LO Opole;
- 2 - Joanna Lisiowska XXI LO Warszawa.
Rozwiązania zadań
Zad. 1. Dziedziną równania jest zbiór R. Jeżeli cosx ∈ C, to [cosx] = cosx i równanie jest równoważne równaniu sinx = 0, stąd x = nπ. Gdzie n ∈ C. Jeżeli 0 < cosx < 1, to [cosx = 0] i równanie jest równoważne równaniu sinx = 0, stąd x ∈ ∅ (gdy sinx = 0, to cosx = -1 lub cosx = 1). Jeżeli -1 < cosx < 0, to [cosx] = -1 i równanie jest równoważne równaniu sinx = -1 – cosx, stąd x ∈ ∅ (jeżeli -1 < cosx < 0 i sinx = -1 – cosx, to korzystając z tożsamości sin2x+ cos2x = 1 otrzymujemy równanie 1 + 2cosx + cos2x + cos2x = 1, czyli cosx(1 + cosx) = 0, a to równanie nie ma rozwiązań, gdyż -1 < cosx <0). Zbiorem rozwiązań jest zbiór {nπ; n ∈ C}
Zad. 2. Liczby pierwsze p i q nie mogą być jednocześnie parzyste i nieparzyste, gdyż wówczas liczba pq + qp byłaby parzysta i większą od 2, a więc nie byłaby liczbą pierwszą. Zatem p = 2 i q ≥ 3 lub p ≥ 3 i q = 2. Jeżeli (p = 2 i q=3) lub (p = 3 i q = 2) to pq + qp = 23+ 32 = 17 i 17 jest liczbą pierwszą. Jeżeli p = 2 i q > 3 to pq + qp = 2q + q2 = (2q + 1)+ (q2 – 1) = (2q + 1)+ (q – 1)(q + 1). Liczba (q – 1)(q + 1) jest podzielne przez 3 (q jako liczba pierwsza większa od 3 nie dzieli się przez 3 zatem jedna z liczb q – 1 lub q + 1 jest podzielna przez 3) oraz 2q + 1 jest podzielne przez 3, ponieważ q jest liczbą nieparzystą. Stąd wynika, ze liczba 2q + q2 jest liczbą złożoną dla każdego q >3. Podobnie dowodzimy, że jeżeli p > 3 i q = 2 to liczba p2 + 2p jest liczbą złożoną dla każdego p > 3 Zatem pq + qp jest liczbą pierwszą tylko wtedy, gdy p = 2 i q =3 lub p = 3 i q = 2
Zad. 3.
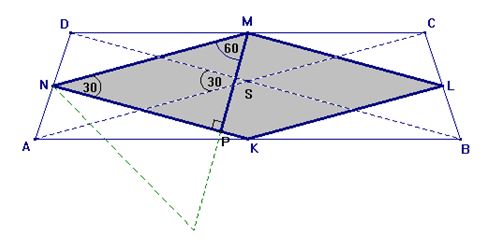
Trapez jest równoramienny, więc przekątne są równe |AC| = |BD|=12 cm. W trójkącie ACD, odcinek MN łączy środki jego boków, więc MN||AC i |MN| = 1/2|AC|. Podobnie w trójkącie ABC AC||KL i |KL| = 1/2|AC| Ponieważ MN||AC i KL||AC więc MN||KL oraz |MN| = 1/2|AC| i |KL|= 1/2|AC|, więc |MN|=|KL|= 1/2|AC| = 6 Podobnie biorąc pod uwagę trójkąty BCD i BDA wykazujemy, że: LM||NK i |LM|=|NK| = |BD|= 6. Czworokąt KLMN jest zatem rombem o boku 6 cm. Ponieważ MN||AC i NK ||BD to ∡ASD = ∡MNK = 300 Zatem kąt ostry rombu wynosi 300. Z wierzchołka M opuszczamy wysokość MP. W trójkącie prostokątnym MPN kąty ostre wynoszą 300 i 600stopni, zatem wysokość rombu, jest równa połowie boku trójkąta równobocznego. |MP| = 1/2|MN|= 3, Wysokość rombu wynosi 3 cm. PKLMN = a . h = 6 . 3 = 18 cm2.
