Zad. 1. Podstawą trójkąta równobocznego jest średnica koła o promieniu r. Oblicz stosunek pola części trójkąta leżącej poza kołem do pola części trójkąta leżącej wewnątrz koła.
Zad. 2. W kulę wpisano stożek, którego przekrój osiowy jest trójkątem równobocznym. Oblicz stosunek pól powierzchni całkowitej stożka i powierzchni kuli.
Zad. 3. Dla jakiej wartości m wykres funkcji y = x+m ma dwa punkty wspólne z okręgiem o promieniu długości 1 i środku w początku układu współrzędnych?
W maju punkty zdobyli:
- 3 pkt. – Bartosz Kaczor I LO Głogów, Kasper Radom II LO Lubin, Laura Stefanowska Katolickie LO Legnica, Aleksandra Strzelecka VIII LO Poznań, Roman Szlachtun LO 9 Wrocław, Wojciech Szwarczyński II LO Wałbrzych, Igor Wojtun I LO Głogów, Kacper Woszczek II LO Wałbrzych;
- 2 pkt. – Mateusz Misztal III LO Kielce;
- 1 pkt. – Karol Czub II LO Oleśnica.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
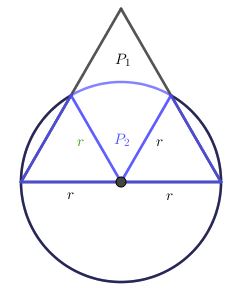
Zad. 1. Oznaczmy: P - pole trójkąta, P1 – pole części trójkąta leżącej poza kołem, P2 – pole części trójkąta leżącej wewnątrz koła. Z warunków zadania mamy:
[tex] P= \frac{(2x)^2\sqrt{3}}{4}=r^2\sqrt{3}[/tex]
[tex] P_2= 2\cdot\frac{r^2\sqrt{3}}{4}+\frac{1}{6}πr^2=\frac{1}{2}r^2\sqrt{3} +\frac{1}{6}\pi r^2[/tex]
[tex] P_1=P-P_2=\frac{1}{2}r^2\sqrt{3} -\frac{1}{6}\pi r^2[/tex]
[tex]\frac{P_1}{P_2}=\frac{\frac{1}{2}r^2\sqrt{3} -\frac{1}{6}\pi r^2}{\frac{1}{2}r^2\sqrt{3} +\frac{1}{6}\pi r^2} =\frac{\frac{1}{6}r^2(3\sqrt{3}-\pi)}{\frac{1}{6}r^2(3\sqrt{3}+\pi)}=\frac{3\sqrt{3}-\pi}{3\sqrt{3}+\pi}[/tex]
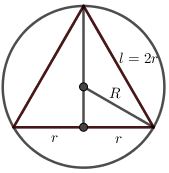
Zad. 2. Oznaczmy: r - promień podstawy stożka, R – promień kuli, h – wysokość trójkąta równobocznego. Wówczas
[tex]R=\frac{2}{3}\cdot h=\frac{2}{3}\cdot\frac{2r\sqrt{3}}{2}=\frac{2}{3}r\sqrt{3}[/tex]
[tex]\frac{P_s}{P_k}=\frac{\pi r^2+\pi rl}{4\pi R^2}=\frac{\pi r^2+\pi r\cdot 2r}{4\pi (\frac{2}{3}r\sqrt{3})^2}=\frac{3\pi r^2}{\frac{16\pi r^2}{3}}=\frac{9}{16}[/tex]
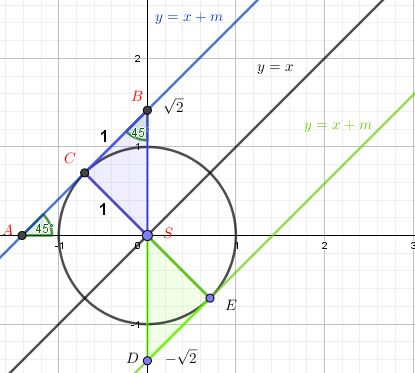
Zad. 3. Prosta y = x+m jest równoległa do prostej y=x i nachylona do osi x pod kątem 45°. Poprowadźmy proste styczne do okręgu i równoległe do prostej y=x. Wówczas trójkąt ASB jest prostokątny, równoramienny o przyprostokątej długości m, a trókąt SBC jest prostokątny, równoramienny o przyprostokątnej długości 1, skąd m = √2. Analogiczne rozumowanie przeprowadzamy dla trójkąta SDE. Dla m=√2 oraz m=-√2 prosta z okręgiem ma jeden punkt wspóny, zatem wykres funkcji y = x+m ma dwa punkty wspólne z okręgiem jeśli m∈(-√2,√2).
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
