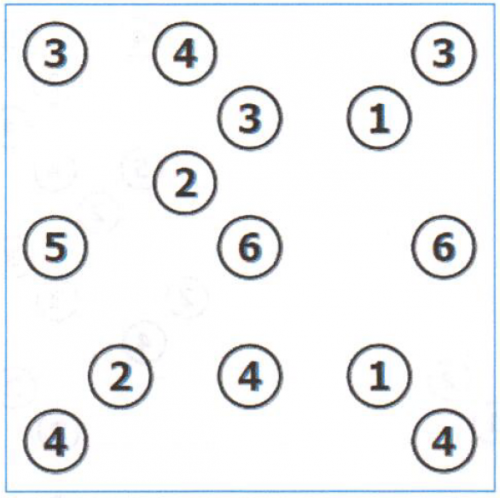
Zad. 1. W łamigłówce "mosty" okrągłe pola zawierają cyfry od 1 do 8 i nazywane są wyspami. Celem zadania jest takie połączenie wszystkich wysp, aby utworzyły jedną spójną grupę. Wyspy łączy się za pomocą mostów (odcinków), które powinny spełniać następujące warunki:
- Muszą zaczynać się i kończyć na różnych wyspach.
- Muszą być odcinkami poziomymi lub pionowymi.
- Nie mogą przecinać żadnego innego mostu ani żadnej wyspy.
- Parę wysp mogą łączyć co najwyżej dwa mosty.
- Liczba mostów wychodząca z jednej wyspy musi być zgodna z liczbą znajdującą się na niej.
Prześlij skan/zdjęcie swojego rozwiązania.
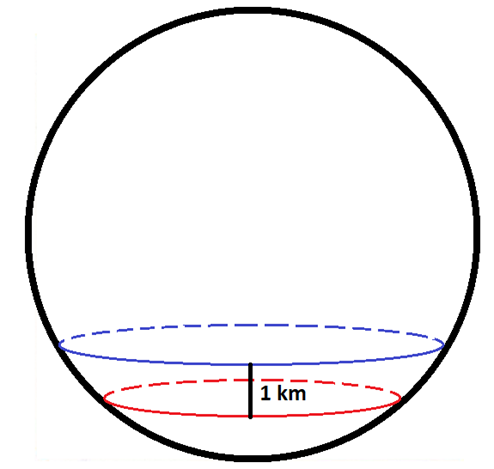
Zad. 2. Myśliwy przeszedł kilometr na południe, skręcił i przeszedł kilometr na wschód, po czym znowu skręcił i przeszedł kilometr na północ. Okazało się, że wrócił do punktu wyjścia, i nie był to wcale biegun północny. Jak to możliwe?
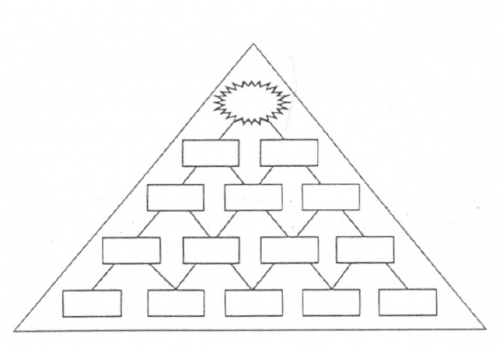
Zad. 3. W pola znajdujące się w podstawie trójkąta wpisz pięć liczb naturalnych, których suma wynosi 25. Kolejne pola wypełniaj w następujący sposób: jeśli sąsiednie liczby są
- parzyste, w pole nad nimi wpisz ich sumę;
- nieparzyste, w pole nad nimi wpisz ich dodatnią różnicę;
- różnej parzystości, w pole nad nimi wpisz ich iloczyn.
Podaj największą liczbę, jaką potrafisz w ten sposób uzyskać na szczycie trójkąta.
W tym miesiącu punkty zdobyli:
- 3 - Daria Bumażnik - doktorantka na Wydziale Chemii UWr, Monika Kosek gospodyni domowa z Wrocławia, Agata Leśnicka - programistka z Poznania, Krystyna Lisiowska - redaktor z Warszawy, Piotr Mazur - specjalista systemów ERP ze Złotoryi, Edward Nowicki - informatyk z Poznania, Andrzej Piasecki - administrator IT z Oleśnicy, Tomasz Tomiczek - nauczyciel z Lipowej, Michał Węgrzyn - ALO PWr Wrocław,
- 2 - Bogusz Boliński I LO Kraków, Joanna Koścień - nauczycielka z Piekar Śląskich, Emilia Stadnicka I LO Kraków,
- 1 - Agata Centkowska - informatyk z Biela, Natalia Lodzińska - SP 41 Kraków.
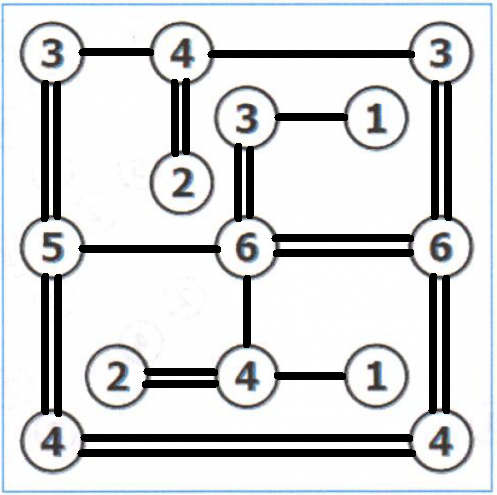
Zad. 1. Rozwiązanie przedstawia rysunek.
Zad. 2. Taka sytuacja mogła mieć miejsce w okolicy bieguna południowego, np. w dowolnym punkcie równoleżnika, który leży w odległości 1 km na północ od równoleżnika o długości 1 km (lub w odległości 1 km na północ od równoleżnika o długości 1/2 km, 1/3 km, ..., 1/n km dla naturalnych wartości n).
Zad. 3. Najwyższy możliwy do uzyskania wynik to 408, otrzymany z układu liczb w podstawie: 1, 6, 11, 6, 1 lub 1, 2, 11, 10, 1. Jeśli dopuścić użycie zera w podstawie, to można osiągnąć wynik 504 z układu w podstawie: 0, 0, 12, 13, 0.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
Pytanie do zadania 3
Czy liczby w dolnym rzędzie powinny być różne? Jeśli nie, to co w przypadku sąsiadujących identycznych liczb nieparzystych?
Odp.
Liczby nie muszą być różne. Algorytm zadziała, jeśli uznać, że zero jest zarówno dodatnie jak i ujemne. Tylko czy warto taki przypadek rozważać w świetle treści zadania?