Zad. 1. W czasie ferii Bolek, Lolek i Tola byli na wycieczce. Wędrowali z wioski A do wioski B. W pewnym momencie Lolek zapytał: "ile już przeszliśmy?". "Jedną trzecią całej drogi" - odpowiedział tajemniczo Bolek. "To znaczy, że zostały nam jeszcze 4 km i tyle, ile już przebyliśmy" - szybko obliczyła Tola. Jaka jest odległość AB?
Zad. 2. Mrówka Kleofas podróżuje po linii układającej się w taki ślimak: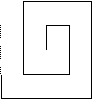 
(każde najbliższe równoległe odcinki leżą w odległości 1 cm). Ile zakrętów zrobi Kleofas, zanim przejdzie pierwszy odcinek prostej o długości 2 m 8 mm?
Zad. 3. Ile razy w ciągu doby wskazówki minutowa i godzinowa zegara się pokrywają?
Styczniowe zadania okazały się na tyle trudne, że nikomu nie udało się poprawnie rozwiązać wszystkich. Tylko Łukasz Kajdan rozwiązał zadanie 2.
Poprawne rozwiązania dwóch zadań nadesłali: Marcin Cichuta z SP 3 w Ścinawie, Marek Kaczmarczyk z SP 3 w Ścinawie, Łukasz Kajdan z SP 82 w Poznaniu, Lilla Łomnicka z SP 3 w Ścinawie, Dominik Miażdżyk z SP 46 we Wrocławiu, Jadwiga Słowik z SP 34 w Gdyni, Anna Zarobnik z SP 3 w Ścinawie.
Gratulujemy!
W klasyfikacji ogólnej prowadzą (na 12 mozliwych pkt.):
Łukasz Kajdan z SP 82 w Poznaniu (11 pkt.), Jadwiga Słowik z SP 34 w Gdyni (11 pkt.), Lilla Łomnicka z SP 3 w Ścinawie (10 pkt.), Weronika Feliszek z SP 3 w Ścinawie (9 pkt.), Marek Kaczmarczyk z SP 3 w Ścinawie (9 pkt.).
Zad. 1. Z rozmów dzieci wynika, że cała ich droga (czyli jej trzy trzecie) to jedna trzecia, 4 km i jeszcze jedna trzecia. Zatem 4 km to jedna trzecia drogi, czyli odległość AB wynosi 12 km.
Zad. 2. Kolejne odcinki mają długości 1 cm, 1cm, 2 cm, 2 cm, 3 cm, 3 cm, 4 cm, 4 cm itd., zatem pierwszy odcinek prostej o długości 2 m 8 mm = 200,8 cm zmieści się w pierwszym odcinku długości 201 cm. Wcześniej Kleofas przejdzie po dwa odcinki o długościach 1, 2, 3 itd. aż do 200 cm, czyli w sumie 400 odcinków, a po każdym z nich musi zakręcić. Zrobi więc 400 zakrętów.
Zad. 3. Wskazówki pokrywają się o północy, potem chwilę po 5 min po pierwszej, chwilę po 10 min po drugiej, chwilę po 15 min po trzeciej, chwilę po 20 min po czwartej, tuż przed wpół do szóstej, trochę po wpól do siódmej, trochę przed za 20 ósma, trochę przed za 15 dziewiąta, trochę przed za 10 dziesiąta, trochę przed za 5 jedenasta i o 12:00, po czym cykl się powtarza. Pokrycie nastąpi więc 2·11=22 razy. Odpowiedzią prawidłową nie jest 24, bo wówczas musiałoby zdarzać się to co godzinę, a zdarza się rzadziej, bo gdy wskazówka minutowa robi pełny obieg tarczy, godzinowa też trochę się przesuwa i jej "ucieka".
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
