I love maths. It's full of pies - mawiają brytyjscy uczniowie, co można przetłumaczyć jako: Lubię matmę, jest pełna ciasteczek ("pie" oznacza w angielskim zarówno ciasteczko jak i literę pi). W tej figlarnej grze słów tkwi jednak ziarno prawdy. Choć może w matematyce trudno znaleźć ciasteczka, ale na pewno w ciasteczkach można doszukać się matematyki.
Herbatniki czy krakersy najczęściej mają kształt rozmaitych wielokątów.
Mogą też mieć kształt koła lub rozety otrzymanej z kilku kół.
Zdarzają się jednak bardziej wyszukane matematyczne kształty. To krakers w kształcie krzywej zwanej asteroidą. Powstaje ona jako ślad punktu na obręczy okręgu toczącego się wewnątrz okręgu o czterokrotnie większym promieniu.
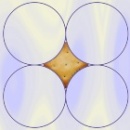
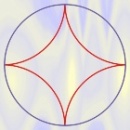
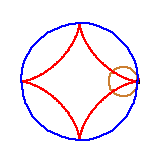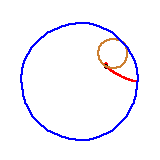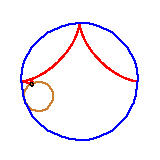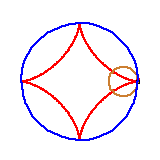
Czy drugi rysunek w powyższym ciągu jest poprawny? Czy asteroida jest rzeczywiście sklejona z czterech łuków okręgów? Oto jest pytanie.
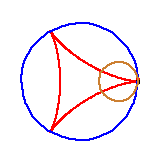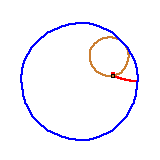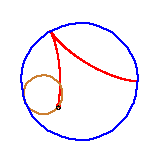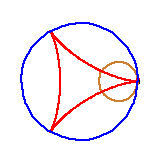
Podobnie powstaje krzywa zwana deltoidą. Ma trzy "wierzchołki", bo powstaje jako ślad punktu na obręczy okręgu toczącego się wewnątrz okręgu o trzykrotnie większym promieniu. Czy deltoida składa się z łuków okręgów?
A jaka krzywa powstanie, gdy obręcz będzie toczyła się wewnątrz okręgu o dwukrotnie większym promieniu? Odpowiedź znajdziesz w arykule Rolling stones (3) - rysują cykloidę.
Czy spotkałeś inne interesujące z matematycznego punktu widzenia ciastka? A ciekawe matematycznie makarony? A inne smakołyki? Napisz do nas!
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
Ciasteczkowi matematycy
Smaki matematyki
Zanim schrupiecie popularne crunchipsy przyjrzyjcie się, że mają kształt paraboloidy hiperbolicznej, zwanej też powierzchnią siodłową. Powierzchnia ta powstaje wskutek przesunięcia paraboli wzdłuż innej paraboli, przy czym obie muszą leżeć w prostopadłych płaszczyznach, mieć równoległe osie symetrii i przeciwnie skierowane ramiona. Czy potrafisz wskazać te parabole na poniższym wykresie?
Więcej na mojej stronie: http://www.tomaszgrebski.pl/viewpage.php?page_id=581