Zad. 1. Punkty E i F są odpowiednio środkami boków BC i CD kwadratu ABCD. Odcinki AE i BF przecinają się w punkcie K. Jaki jest stosunek pól trójkąta AKF i czworokąta KECF?
Zad. 2.Na płaszczyźnie danych jest n>3 punktów nie leżących na jednej prostej. Wykaż, że istnieje okrąg przechodzący przez 3 z nich niezawierający wewnątrz żadnych pozostałych punktów.
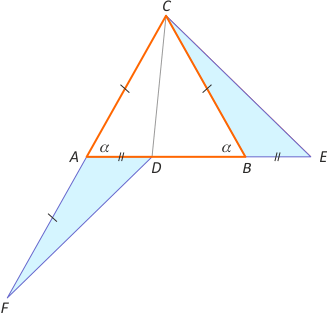
Zad. 3. Na podstawie AB trójkąta równoramiennego ABC obrano punkt D, a na przedłużeniu AB poza wierzchołek B obrano punkt E, tak że |AD| = |BE|. Wykaż, że |CD|+|CE| > |CA|+|CB|.
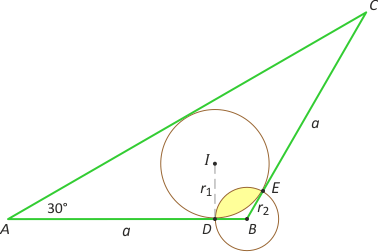
Zad. 4. (wolna amerykanka) W trójkącie ABC zachodzi |AB|=|BC|=a i kąt ABC ma 120°. W trójkąt ten wpisano okrąg styczny do boku AB w punkcie D. Drugi okrąg - o środku w B - przechodzi przez punkt D. Oblicz pole części wspólnej kół ograniczonych tymi okręgami.
W grudniu punkty za zadania 1 - 3 otrzymali:
- 30 - Michel Migas (student PW),
- 28 - Dominik Bysiewicz (I LO Krosno), Krzysztof Lis (XIV LO Warszawa) oraz Tadeusz Porzucek (emerytowany nauczyciel, Gostyń),
- 20 - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Adam Wrzesiński (terapeuta z Bielska-Białej) oraz Karolina Wlaź (studentka UMCS),
- 18 - Jerzy Kawka (I LO Kraków),
- 12 - Kamil Rozbicki (student WSH we Wrocławiu),
- 10 - Krzysztof Mach (I LO Kraków).
Punkty za zadanie 4 otrzymali:
- 10 - Jacek Bagiński, Dominik Bysiewicz, Zygmunt Krawczyk (nauczyciel, SLO Żary), Tadeusz Porzucek oraz Krzysztof Lis,
- 2 - Michel Migas.
Gratulacje!
W Nowym Roku życzymy dużo zdrowia i ciekawych pomysłów na rozwiązania kolejnych zadań z Ligi.
Zad. 1. Niech S oznacza pole figury. Zauważmy, że SKECF : SAKF = (SAECF–SAKF) : SAKF = SAECF/SAKF – 1 = (SABCD–SAFD–SABE)/SAKF – 1 = 1/2SABCD/SAKF – 1. Z podobieństwa trójkątów MKF i KBE mamy |FK|/|KB| = 3/2. Dalej SAKF = SAFB–SABK = 3/5SABF = 3/10SABCD. Zatem SKECF : SAKF = 1/2SABCD : 3/10SABCD – 1 = 2/3. Ostatecznie szukany stosunek SAKF : SKECF wynosi 3:2.

Zad. 2. Niech A i B będą punktami, których wzajemna odległość jest najmniejsza. Rozważmy okrąg o średnicy AB. Oczywiście wewnątrz tego okręgu nie leży żaden z danych punktów. Niech C będzie punktem, z którego odcinek AB jest widoczny pod największym kątem. Wówczas wewnątrz okręgu przechodzącego przez punkty A, B i C nie ma innych spośród danych punktów.
Zad. 3. Niech F leży na przedłużeniu boku AC i |AC| = |AF|. Zauważmy, że |∡FAD| = |∡CBE|. Stąd na mocy cechy bkb trójkąty FAD i CBE są przystające. Łatwo zauważyć, że |AC| + |BC| = |CF| < |FD| + |CD| = |CD| + |CE|, co kończy dowód.
Zad. 4. Szukane pole jest równe sumie pól dwóch odcinków kołowych. Zauważmy, że |DB| = r2 = p – |AC| (gdzie p oznacza połowę obwodu trójkąta ABC - patrz rozwiązanie zad. 4 z marca 2015). Zatem r2 = a(2–√3)/2. Z drugiej strony r1 = √3|DB| z trójkąta ekierkowego IDB. Mamy r1 = a(2√3–3)/2. Kąt DIE ma miarę 60°, a kąt DBE 120°. Ostatecznie szukane pole S wynosi (1/6)πr12 – SIDE + (1/3)πr22 – SDBE. Po nietrudnych obliczeniach otrzymujemy S = a2(7–4√3)(5π/6 – √3)/4.