Każdy pracownik odkłada obowiązkowo część swojej pensji na swój kapitał emerytalny. Kiedy przestanie pracować po osiągnięciu tzw. wieku emerytalnego (który wynosi obecnie dla kobiet 60, a dla mężczyzn 65 lat) z odłożonej kwoty co miesiąc otrzyma wypłatę, nazywaną emeryturą.
Wysokość należnej miesięcznej emerytury jest obliczana w skomplikowany sposób. My założymy, że w momencie przejścia na emeryturę uzbierany kapitał dzieli się przez przewidywany przeciętny czas dalszego życia danej osoby wyrażony w miesiącach i taką kwotę co miesiąc się jej wypłaca. W rzeczywistości uwzględnia się jeszcze inflację, czyli utratę wartości nabywczej pieniędzy odłożonych w kapitale emerytalnym. Dlatego emerytury są waloryzowane, tzn. podnoszone o kwotę inflacji.
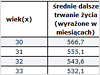
Aktualne dane o przeciętnej długości życia kobiet i mężczyzn można znaleźć w corocznych publikacjach Głównego Urzędu Statystycznego (GUS) - tzw. tablicach trwania życia. Są one tworzone za pomocą zaawansowanych metod statystycznych. Poniżej prezentujemy fragment takiej tabeli.
| wiek osoby w 2010 roku w latach |
mężczyźni |
kobiety |
|
| 60 | 18,25 | 23,47 | |
| 62 | 16,94 | 21,82 | |
| 65 | 15,06 | 19,39 | |
| 67 | 13,86 | 17,81 |
Przykład 1. Jakiego wieku powinna średnio dożyć kobieta, która w grudniu 2010 roku skończyła 65 lat? Przez ile miesięcy powinna ona średnio pobierać emeryturę?
Rozwiązanie. Szacowany czas trwania życia takiej kobiety to 19,39 lat, czyli 19 lat i
12·0,39=4,68 miesięcy. Zatem dożyje ona średnio 65+19,39 = 84 lat i 4,68 miesięcy i będzie pobierała emeryturę jeszcze przez 19·12+5 = 233 miesiące. Zakładając, że jest od pięciu lat na emeryturze, łącznie powinna pobierać emeryturę przez 233+5·12 = 293 miesiące.
Przykład 2. Mężczyzna przeszedł na emeryturę w wieku 65 lat w styczniu 2011 roku. Przez lata pracy uzbierał kapitał emerytalny w wysokości 300 000 zł. Ile wyniesie jego miesięczna emerytura?
Rozwiązanie. Przeciętne dalsze trwanie życia takiego mężczyzny wynosi 15,06·12 = 180,72 miesiące. Zatem przypuszczalnie będzie on pobierał emeryturę przez 181 miesięcy. Powinna ona wynosić 300000:181 = 1657,46 zł.
Ostatnio wiele się dyskutuje o planowanej reformie emerytalnej. Jest ona potrzebna, bo Polacy żyją coraz dłużej, a więc przez coraz dłuższy czas pobierają emerytury. Jeśli ich uzbierany kapitał będzie mały, a liczba wypłat duża, wysokość emerytury będzie bardzo niska i pieniędzy nie wystarczy na cały miesiąc.
[koniec wykładu dla SP]
Głównym celem reformy jest podniesienie wieku przejścia na emeryturę (dla kobiet i mężczyzn) do 67 lat. Dodatkowo planuje się wprowadzenie możliwości wcześniejszego przechodzenia na emeryturę kobiet w wieku 62 i mężczyzn w wieku 65 lat. Jednak, aby móc przejść na wcześniejszą emeryturę, należy przepracować co najmniej 35 lat. W tym okresie emerytura byłaby wypłacana w wysokości 50% tej, jaką otrzymałby pracownik w wieku 67 lat. Jednak po 67 roku życia emerytura nie wróciłaby już do poziomu 100%, gdyby została uszczuplona w okresie wcześniejszym. Kapitał emerytalny byłby wtedy pomniejszony o łączną kwotę pobranych wcześniejszych emerytur.
Przykład 3. Gdyby kobieta, która uzbierała kapitał w wysokości 400 000 zł, postanowiła przejść na wcześniejszą emeryturę na zasadach proponowanych w reformie w wieku 62 lat, to jaką emeryturę będzie pobierać do 67 roku życia, a jaką później, gdy jej dalszy czas trwania życia powyżej wieku 67 lat wynosi 200 miesięcy?
Rozwiązanie. Przechodząc na emeryturę w wieku 67 lat, kobieta dostałaby: 400000:200 = 2000 zł emerytury. Przechodząc na wcześniejszą emeryturę w wieku 62 lat, będzie przez 5 lat dostawała połowę tej kwoty, czyli 1000 zł. Przez te lata wykorzysta z kapitału emerytalnego 5·12·1000 = 60000 zł. Zostanie jej 400000-60000 = 340000 zł kapitału emerytalnego i 200 miesięcy do przeżycia, czyli po 67 roku życia będzie dostawała 340000:200 = 1700 zł. Zatem kobieta otrzyma po 67 roku życia co najmniej 300 zł emerytury mniej niż gdyby nie przeszła na wcześniejszą emeryturę (co najmniej, bo przez 5 lat dodatkowej pracy wzrósłby jeszcze jej kapitał emerytalny).
Zadanie 1. Korzystając z tabeli przeciętnego dalszego trwania życia, oblicz, do jakiego wieku średnio będą dożywali mężczyźni i kobiety, którzy obecnie mają 60, 62, 65 i 67 lat. Czy można zaobserwować w tych wynikach jakąś zależność?
Zadanie 2. Pan Zenon, pracując przez całe dorosłe życie, uzbierał kapitał emerytalny w wysokości 200 000 zł. W wieku 65 lat w roku 2011 przeszedł na emeryturę. Oblicz, ile będzie wynosiła jego miesięczna wypłata.
Zadanie 3. Jaki kapitał emerytalny powinna uzbierać pani Leokadia, która przeszła na emeryturę w 2011 roku w wieku 60 lat, aby wysokość jej wypłaty wynosiła 1500 zł miesięcznie? A ile powinien uzbierać jej mąż przechodzący w tym samym roku na emeryturę w wieku 65 lat, aby dostawać taką samą wypłatę? Wyjaśnij, skąd bierze się różnica w wynikach.
Zadanie 1. Podana wyżej tabela przeciętnego dalszego trwania życia nie jest kompletna. Zakładając, że pomiędzy podanymi w niej wartościami funkcja ta zmienia się liniowo, oblicz wartość przeciętnego dalszego trwania życia dla mężczyzny w wieku 66 lat i dla kobiety w wieku 61 lat.
Zadanie 2. Gdyby pan Zenon po reformie emerytalnej zdecydował się przejść na wcześniejszą emeryturę w wieku 65 lat, z wypracowanym kapitałem emerytalnym w wysokości 200 000 zł, to ile będzie wynosiła jego emerytura w wieku 65-67 lat, a ile po 67 roku życia? Zakładamy, że w dniu przejścia pana Zenona na emeryturę, przewidywany dalszy czas trwania życia 67-letniego mężczyzny wynosił 194 miesiące. O ile mniejsza będzie jego emerytura w drugim okresie w porównaniu z tą, którą otrzymałby, gdyby poczekał do pełnego wieku emerytalnego? Zakładamy, że przez te dwa lata dodatkowej pracy jego kapitał emerytalny wzrósłby jeszcze o 10000 zł.
Zadanie 3. Pani Leokadia wie, że po reformie jej kapitał emerytalny pozwoli jej po przejściu na wcześniejszą emeryturę w wieku 62 lat uzyskać 500 zł emerytury w okresie 62-67 lat. Ile pieniędzy odłożyła pani Leokadia w kapitale emerytalnym, jeśli jej dalszy czas życia po 67 roku szacowany jest na 220 miesięcy? Jaką emeryturę będzie miała pani Leokadia po 67 roku życia?
Zadanie 1. Z danych GUS wynika, że w ostatnim dwudziestoleciu przeciętna długość dalszego trwania życia dla 60-letniej kobiety wzrosła o 3,5 roku. O ile procent mniejszą emeryturę dostaje 60-letnia kobieta, która przeszła na emeryturę w 2011 roku od kobiety, która z takim samym wypracowanym kapitałem emerytalnym przeszła na emeryturę w 1991 roku? O ile procent kapitał emerytalny 60-letniej kobiety w 2011 roku musi być większy, aby otrzymała taką samą emeryturę, jak jej poprzedniczka 20 lat wcześniej?
Zadanie 2. W 2011 roku 67-letni pan Zenon przeszedł na emeryturę z kapitałem 200 000 zł. Wysokość miesięcznej emerytury zawsze oblicza się tak, aby kapitał wczerpał się po przewidywanym okresie dalszego trwania życia. Jednak kapitał pana Zenona jest ulokowany na specjalnym koncie emerytalnym z roczną stopą procentową 2% i miesięczną kapitalizacją odsetek. Zatem co miesiąc będzie pomniejszany o wypłacaną emeryturę, ale i zasilany przez odsetki, co należy uwzględnić, obliczając stałą wysokość jego emerytury. O ile miesięczna emerytura pana Zenona będzie wyższa niż w przypadku gdyby jego kapitał emerytalny nie został ulokowany na koncie emerytalnym?
Zadanie 3. Pani Leokadia po reformie emerytalnej w wieku 65 lat straciła pracę, mając uzbierany kapitał emerytalny w wysokości 200 000 zł. Ma do wyboru dwie opcje: albo przejść na wcześniejszą emeryturę, albo poczekać dwa lata na bezrobociu i dopiero wtedy przejść na emeryturę. Szacowana długość życia dla 65-letniej kobiety wynosi 80 lat. Jaką łączną kwotę emerytur pobierze pani Leokadia w obu przypadkach, jeśli dożyje 80 urodzin?
W tym miesiącu 3 punkty zdobyli: Aleksander Cząstkiewicz-Trawiński SP 14 Głogów, Adam Gawlik SP 28 Wałbrzych, Anna Górska SP 2 Olesno, Joanna Lisiowska KSP Warszawa, Aleksandra Piasecka KSP Oleśnica i Mateusz Rzepecki SP 91 Wrocław.
2,5 punktu otrzymali: Igor Rosiak SP 28 Wałbrzych i Andrzej Turko SP Optimum Wrocław.
1,5 punktu otrzymał: Wojciech Henik PSP Mieroszów.
Pozostałym uczestnikom punktów w tym miesiącu nie przyznano.
Po siedmiu miesiącach Ligi z wynikiem 21 pkt. prowadzi: Joanna Lisiowska KSP Warszawa.
W tym miesiącu 3 punkty zdobyli: Daria Bumażnik GM 1 Jelenia Góra, Liwia Ćwiek GM 2 Złotoryja, Mieszko Gałat GM 50 Bydgoszcz i Anna Łeń GM 1 Łódź.
2,5 punktu zdobyli: Krzysztof Bednarek GM 13 Wrocław, Krzysztof Danielak GM 1 Jelenia Góra, Wojciech Górski GM 2 Olesno i Bartosz Sójka GM 1 Jelenia Góra.
2 punkty uzyskała Aleksandra Polcyn GM Akademickie Toruń.
Pozostałym uczestnikom nie przyznano w tym miesiącu punktów.
Po siedmiu miesiącach Ligi z wynikiem 20,5 pkt. prowadzi Anna Łeń GM 1 Łódź.
W tym miesiącu 2 punkty zdobyli: Paweł Samoraj I LO Olsztyn i Tomasz Skalski III LO Wrocław.
1,5 punktu zdobył Maciej Pomykała Liceum Akademickie Toruń.
1 punkt zdobyli: Aleksandra Pawłowska XIV LO Wrocław, Bartłomiej Polcyn I LO Inowrocław i Dominik Zygmunt TE Biała Rawska.
Pozostali uczestnicy nie otrzymali w tym miesiącu punktów.
Po siedmiu miesiącach Ligi z wynikiem 17 pkt. prowadzi: Maciej Pomykała LA Toruń.
Zad. 1. Mężczyźni statystycznie dożyją będą wieku:
60 + 18,25 = 78,25 lat,
62 + 16,94 = 78,94 lat,
65 + 15,06 = 80,06 lat,
67 + 13,86 = 80,86 lat.
Kobiety średnio żyją dłużej niż mężczyźni i dożyją wieku:
60 + 23,47 = 83,47 lat,
62 + 21,82 = 83,82 lat,
65 + 19,39 = 84,39 lat,
67 + 17,81 = 84,81 lat.
Z wyników widać, że im ktoś w 2010 roku miał więcej lat, tym średnio dożyje starszego wieku.
Zad. 2. Przeciętny czas dalszego trwania życia pana Zenona (patrz tabela) wynosi 15,06·12 = 180,72 miesiące. Zatem będzie on pobierał emeryturę przez 181 miesięcy. Jego emerytura po zaokrągleniu do groszy będzie wynosiła 200 000 : 181 = 1104,97 zł.
Zad. 3. Przeciętne czas dalszego trwanie życia pani Leokadii wynosi 23,47·12 = 281,64 miesiące. Zatem będzie ona pobierała emeryturę przez 282 miesiące. Powinna uzbierać kapitał 282 · 1500 = 423 000 zł. Przeciętny czas dalszego trwania życia męża pani Leokadii wynosi 15,06·12 = 180,72 miesiące. Zatem będzie on pobierał emeryturę przez 181 miesięcy. Powinien uzbierać kapitał 181 · 1500 = 271 500 zł. Różnica bierze się stąd, że pani Leokadia będzie pobierała emeryturę przez 101 miesięcy więcej niż jej mąż, ponieważ przeszła na emeryturę 5 lat wcześniej, a dodatkowo przeciętna długość życia kobiet jest większa niż mężczyzn.
Zad. 1. Mężczyźnie w wieku 66 lat zostanie (15,06+13,86)/2 = 14,46 lat życia, a kobiecie w wieku 61 lat (23,47+21,82)/2 = 22,645 lat życia.
Zad. 2. Gdyby pan Zenon przeszedł na wcześniejszą emeryturę w pierwszym okresie otrzymywałby 200000/(2·194) = 515,46 zł, a w drugim (200000 - 24·515,46)/194 = 967,16. W przypadku przejścia na emeryturę w wieku 67 lat otrzymywałby 210000/194 = 1082,47 zł, czyli o 115,31 zł więcej.
Zad. 3. Pani Leokadia odłożyła w kapitale emerytalnym 2·500·220 = 220 000,00 zł. Jeśli przejdzie na wcześniejszą emeryturę, to po 67 roku życia otrzyma emeryturę w wysokości (220000-500·60)/220 = 863,64 zł.
Zad. 1. Kobieta przechodząca na emeryturę w 2011 roku otrzyma ją mniejszą o 14,91% od swojej rówieśniczki w 1991 roku. Aby ich emerytury były równe, jej kapitał emerytalny musi zwiększyć się o 17,53%.
Zad. 2. Emerytura pana Zenona będzie większa miesięcznie o około 175,38 zł, przy zaokrągleniu przeciętnego czasu życia 67-latka do 167 miesięcy.
Zad. 3. Jeśli pani Leokadia przejdzie na wcześniejszą emeryturę, dostanie łącznie 149 018,23 zł. Jeśli poczeka na bezrobociu, dostanie łącznie 145 985,40 zł.
Co to za podejście?
To podejście może nadaje się na ćwiczenia arytmetyczne, ale nie na wyjaśnianie kwestii reformy emerytalnej... Bo ta powinna być rozpatrywana oczywiście jako zadanie z rachunku prawdopodobieństwa. Patrząc z perspektywy obywatela, co tutaj rzekomo się robi, należy wziąć pod uwagę prawdopodobieństwo dożycia / niedożycia do wieku emerytalnego i starszego, a nie średni czas życia.
Przecież o to chodzi!
Tabele ustalające średni czas życia osoby w danym wieku opracowywane są przecież właśnie za pomocą zaawansowanych metod, nie tyle rachunku prawdopodobieństwa, co raczej statystyki. Zajmują się tym aktuariusze. A potem każdy zainteresowany tematem może z nich korzystać i szacować swoją emeryturę, bez konieczności znajomości tej całej zaawansowanej matematyki. Tak to zazwyczaj działa w życiu - potrafisz obsłużyć telefon komórkowy, a wiesz, jaka matematyka się w tym kryje? Nie, bo i po co...
TTŻ
Chyba odpowiedź została już za mnie udzielona. Dodam tylko, że Liga przeznaczona jest dla uczniów (począwszy od uczniów SP), a nie dla studentów matematyki. Trudno jest mówić o rachunku prawdopodobieństwa w szkole, gdy nawet nie wszyscy studenci kierunków ścisłych są uczeni prawdopodobieństwa. Zadania zawsze poprzedzane są miniwykładem, który ma na celu naświetlić w miarę prosty sposób dany temat. Mają popularyzować matematykę finansową wśród młodzieży i nie pretendują do uniwersyteckiego wykładu z matematyki ubezpieczeń na życie.
Proaganda?
Halo, halo, tu nie chodzi o byle jakie rachunki, tylko o zadanie, z którego treści jasno widać, że jawi się jako uzasadnienie reformy, przypadkiem akurat przeprowadzanej. Propaganda? Ależ nie, my tylko uczymy odkrywania i rozumienia otaczającego nas świata. To dlaczego nie robić tego uczciwie? Dlaczego nie zapytać, jakie jest prawdopodobieństwo, że pan Zenon (zad.2 GM) nie dożyje wieku 67 lat i cały jego kapitał przepadnie. Zadania skierowane są do uczniów... Powiedziałabym, że z punktu widzenia dydaktyki podejmowanie tego pasjonującego dla ucznia podstawówki czy gimnazjum tematu (och, komuż, gdy dziecięciem był, nie spędzała snu z powiek wysokość jego przyszłej emerytury) może budzić wątpliwości.
TTŻ2
Na temat prawdopodobieństwa w gimnazjum już pisałem wyżej i uważam temat za wyczerpany. Co do propagandy - bez komentarza. Liga stara się co miesiąc nawiązywać do aktualnych tematów, obecnych akurat w mediach. To przyczynia się do reklamy naszej ligi, ale także pomaga zrozumiec młodym ludziom aktualne doniesienia prasowe i telewizyjne. Przykładem mogą być zeszłoroczne wybory i liga o finansowaniu ugrupowań politycznych.