Podatkiem leśnym obłożone są grunty sklasyfikowane w ewidencji gruntów i budynków danej gminy jako lasy. Płatnikiem podatku leśnego jest właściciel lub użytkownik wieczysty lasu. Las może należeć zarówno do osoby prywatnej, osoby prawnej (np. firmy) jak i do skarbu państwa. Lasy należące do państwa w większości pozostają pod zarządem Państwowego Gospodarstwa Leśnego Lasy Państwowe.
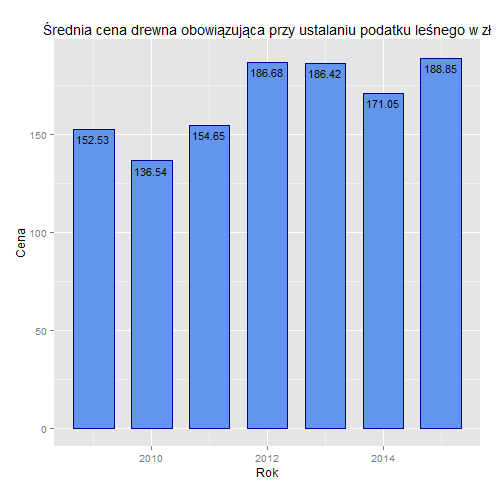
Sposób obliczania rocznej kwoty podatku leśnego jest znacznie prostszy od obliczania podatku rolnego (o którym była mowa w lutym). Wystarczy pomnożyć równowartość pieniężną 0,22 m3 drewna obliczaną według średniej ceny sprzedaży drewna uzyskanej przez nadleśnictwa za pierwsze trzy kwartały roku poprzedzającego dany rok podatkowy przez powierzchnię posiadanego lasu wyrażoną w hektarach (prawdziwych, a nie przeliczeniowych - to dlatego metoda jest prostsza w porównaniu z podatkiem rolnym). Średnią cenę drewna ustala Główny Urząd Statystyczny i publikuje ją nie później niż 20 października roku poprzedzającego rok podatkowy. Średnia cena drewna podana przez GUS jest ceną netto, czyli nie zawiera podatku VAT.
Leśnicy klasyfikują wiek lasów w klasach o rozpiętości 20 lat, stąd klasa I oznacza las w wieku do 20 lat, klasa II - w wieku 21-40 lat, a klasa III oznacza las w wieku 41-60 lat itd. Z podatku leśnego zwolnione są lasy z drzewostanem w wieku do 40 lat oraz lasy wpisane do rejestru zabytków i użytki ekologiczne. Dodatkowo zwolnione z płacenia tego podatku są uczelnie, instytuty badawcze i naukowe, szkoły i zakłady pracy chronionej. Lasy ochronne (np. pełniące cele wodochronne lub glebochronne) oraz lasy położone w rezerwatach przyrody i parkach narodowych są obłożone połową stawki podatku leśnego.
Podatek leśny jest płacony urzędowi gminy, na terenie której las jest położony. Osoby fizyczne płacą go w czterech równych ratach do 15 marca, 15 maja, 15 września i 15 listopada, a osoby prawne, w tym Lasy Państwowe, płacą podatek leśny w ratach miesięcznych do 15 dnia każdego miesiąca.
Przykład 1. Oblicz wysokość podatku leśnego należnego za 5 ha 60-letniego lasu sosnowego w 2015 roku, któremu nie przysługuje żadne zwolnienie podatkowe.
Rozwiązanie. Po uwzględnieniu powierzchni i wieku lasu podatek ten wynosi 5·0,22·188,85 = 207,735 ≈ 207,74 zł.
Lesistość kraju to wskaźnik procentowy pokazujący, jaką część danego kraju stanowią lasy. W 2013 roku lesistość Polski wynosiła 29,4%. Celem na rok 2020 określonym w "Krajowym programie zwiększenia lesistości" jest osiągniecie w Polsce stanu lesistości 30%, a na rok 2050 - stanu 33%.
Zadanie 1. Powierzchnia lasów w Karkonoskim Parku Narodowym w roku 2014 wynosiła 4038,1 ha. Oblicz, jaki roczny podatek leśny zapłaciła dyrekcja Parku w 2014 roku.
Zadanie 2. W 2013 roku Lasy Państwowe sprzedały ogółem 37 076,4 tys. m3 drewna oraz zapłaciły łącznie 167,6 mln zł podatku leśnego. Przyjmijmy, że średnia cena sprzedaży drewna z Lasów Państwowych była taka, jak średnia cena drewna podana przez GUS oraz że poza tym Lasy państwowe nie uzyskały innych przychodów. Jaką część przychodów Lasów Państwowych w 2013 roku wydano na podatek leśny?
Zadanie 3. Jan Dąbrowa posiada obecnie 3,45 ha lasu, w tym 1,05 ha stanowią zeszłoroczne nasadzenia, 1,3 ha to 35-letnia dębina, 0,9 ha to las świerkowy zasadzonego przez jego dziadka trzy lata temu i 0,2 ha porastają 41-letnie olchy. Ile podatku leśnego zapłaci pan Dąbrowa w 2015 roku? A ile zapłacił w 2013 roku?
Zadanie 1. Średni roczny przyrost pozyskanego drewna z Lasów Państwowych kolejno w latach 2009-2013 to odpowiednio: 617 tys. m3, 54 tys. m3, 1940 tys. m3, 536 tys. m3 i 1185 tys. m3. Na ile lat opłacania podatku leśnego pozwolą te przyrosty, jeśli średnia powierzchnia lasów państwowych w tych latach wynosiła 7071,8 tys. ha, a gospodarstwo nie korzystało z żadnych zwolnień i ulg podatkowych?
Zadanie 2. Lasy ochronne w województwie dolnośląskim w 2013 roku stanowiły 62,1% ogólnej powierzchni lasów równej 591,9 tys. ha. O jaką kwotę będzie obniżony podatek leśny należny gminom leżącym w województwie dolnośląskiego z tytułu lasów ochronnych?
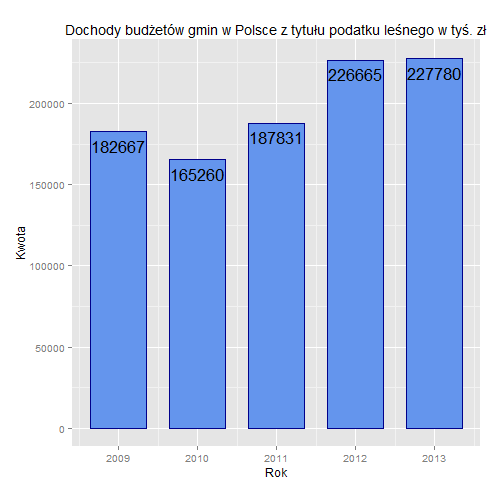
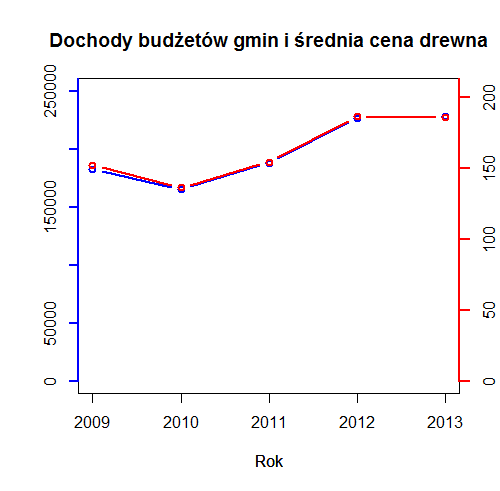
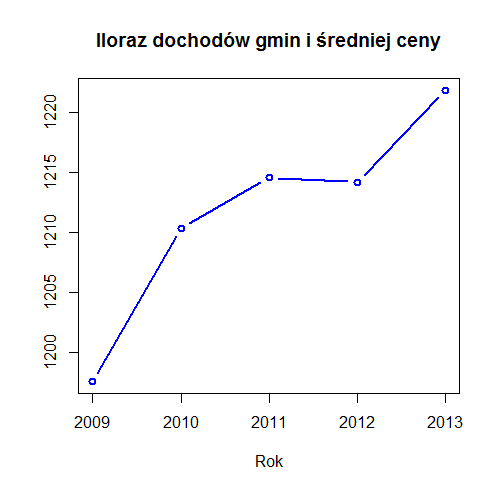
Zadanie 3. Poniższy wykres przedstawia dochody budżetów gmin w Polsce z tytułu podatku leśnego w latach 2009-2013. Zakładając, że w tym czasie procentowy udział ulg w podatku leśnym nie uległ zmianie, czy można wywnioskować coś o zmianie lesistości kraju? Odpowiedź uzasadnij.
Zadanie 1. W nadleśnictwie Złotoryja udział klas wieku w drzewostanie w roku 2011 wynosił: I klasa 0,19%, II klasa 6,99%, III klasa 20,61%, IV klasa 17,69%, V klasa 21,23% i VI klasa i starsze 33,29%. Powierzchnia całkowita lasów tego nadleśnictwa w 2011 roku wynosiła 19148,57 ha, z tego lasy ochronne zajmowały 13572,65 ha, a rezerwaty przyrody - 146,91 ha (przyjmijmy, że są to lasy co najmniej w III klasie wieku). Oblicz wysokość miesięcznej raty podatku leśnego płaconego w 2011 roku przez nadleśnictwo Złotoryja łącznie wszystkim gminom, na których terenie ono leżało.
Zadanie 2. W 2006 roku Lasy Państwowe zarządzały 7043 tys. ha lasów o łącznej zasobności drewna równej 1629,3 mln m3. W 2013 roku powierzchnia lasów zarządzanych przez Lasy Państwowe wynosiła 7079 tys. ha i miały one zasobność drewna równą 1821,7 mln m3. Jaką część powierzchni Polski stanowiły lasy państwowe w 2006, a jaką w 2013 roku? Załóżmy, że zasobność drewna w lasach innych właścicieli w Polsce jest na tym samym poziomie, co zasobność Lasów Państwowych. Ile będzie wynosiła zasobność drewna w polskich lasach w 2020 roku, jeśli osiągniemy cele "Krajowego programu zwiększenia lesistości"? Czy przyrost zasobności drewna pomiędzy rokiem 2013 i 2020 będzie proporcjonalny do tego pomiędzy rokiem 2006 i 2013?
Zadanie 3. W celu obliczenia podatku leśnego stosuje się współczynnik przeliczeniowy 0,22 m3 na hektar lasu. Metr sześcienny to objętość sześcianu o krawędzi długości 1 m. Gdy kupujemy drewno od leśniczego (np. na opał do kominka) kwota na rachunku (zwanym asygnatą) jest wyliczana jako iloczyn ceny drewna i liczby m3 drewna. Jednak gdy pojedziemy do lasu po odbiór kupionego drewna, czekający na nas stos ma objętość większą niż liczba m3 na rachunku. Dzieje się tak dlatego, że na rachunku widnieje cena za 1 m3 czystego drewna, bez kory i powietrza znajdującego się między pniami w stosie. Leśnicy dla odróżnienia objętości drewna z rachunku (w m3) od objętości drewna w stosie stosują pojęcie metra przestrzennego (ozn. mp). W celu porównania tych jednostek stosuje się przelicznik 1 mp = 0,7 m3 dla gatunków: buk, grab, świerk i jodła. Sprawdź, ile metrów sześciennych ma 1 metr przestrzenny drewna bukowego w stosie składającym się z metrowej długości wałków (przybliż je przez walce): 1 wałka o promieniu 50 cm, 4 wałków o promieniu 25 cm, 9 wałków o promieniu 1/6 m i 16 wałków o promieniu 12,5 cm. Następnie powtórz obliczenia, odejmując od każdego wałka drewna korę o grubości 1 cm.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Jakub Ptak SP 64 Wrocław i Adam Stachelek SP 301 Warszawa;
- 2,5 pkt. - Natalia Kiszkowiak SP 66 Warszawa, Bartosz Szczerba SP 35 Szczecin i Roman Zaborowski SP 2 Syców;
- 1 pkt. - Mieszko Baszczak SP 301 Warszawa;
- 0,5 pkt. - Kacper Kobyłecki PSP Bolesławiec.
Po siedmiu miesiącach Ligi z Matematyki Finansowej z wynikiem 20 pkt. (na 21 możliwych) prowadzi Natalia Kiszkowiak. Na drugim miejscu z wynikiem 19,5 pkt. są: Adam Stachelek i Bartosz Szczerba. Na trzecim miejscu z wynikiem 19 pkt jest Jakub Ptak.
Gratulujemy!
W tym miesiącu punkty zdobyli:
- 2,5 pkt. - Kacper Toczek GM 2 Wołów,
- 2 pkt. - Joanna Lisiowska KZE Warszawa,
- 1,5 pkt. - Aleksandra Domagała GM 23 Wrocław,
- 1 pkt. - Jakub Czerniak GM 5 Opole.
Po siedmiu miesiącach Ligi z Matematyki Finansowej z wynikiem 16 pkt. (na 21 możliwych) prowadzi Joanna Lisiowska. Na drugim miejscu jest Kacper Toczek z wynikiem 15,25 pkt., a na trzecim miejscu jest Aleksandra Domagała z wynikiem 15 pkt.
Gratulujemy!
W tym miesiącu punkty zdobyli:
- 3 pkt. - Tomasz Stempniak I LO Ostrów Wielkopolski;
- 2,5 pkt. - Daria Bumażnik II LO Jelenia Góra i Wojciech Wiśniewski I LO Giżycko;
- 1,5 pkt. - Kinga Kurzawa ZS w Ostrzeszowie i Dominika Nowak ZS Ostrzeszów;
- 1 pkt. - Anna Jakubczak I TE Ostrzeszów.
Pozostałym uczestnikom Ligi nie przyznano punktów.
Po siedmiu miesiącach Ligi z Matematyki Finansowej z wynikiem 18,5 pkt. (na 21 możliwych) prowadzi Tomasz Stempniak. Na drugim miejscu jest Daria Bumażnik z wynikiem 15 pkt., a na trzecim miejscu jest Wojciech Wiśniewski z wynikiem 12,25 pkt.
Gratulujemy!
Zad. 1. W 2014 dyrekcja Parku zapłaciła 4038,1·0,22·171,05·0,5 ≈ 75 978,87 zł podatku leśnego.
Zad. 2. Przychody Lasów Państwowych wynosiły 37 076 400 · 186,42 = 6 911 782 488 zł, w tym podatek leśny stanowił 167600000/6911782488 = 20950000/863972811 ≈ 0,02425, czyli podatek leśny stanowił mniej niż 2,5% przychodów Lasów Państwowych w 2013 roku.
Zad. 3. W 2013 roku Jan Dąbrowa nie zapłacił w ogóle podatku leśnego, ponieważ wtedy żaden z jego lasów nie miał więcej niż 40 lat. W 2015 zapłacił podatek tylko za 0,2 ha lasu olchowego i wyniósł on 0,2·0,22·188,85 ≈ 8,31 zł.
Zad. 1. Łączny przyrost pozyskanego drewna to 4 332 tysięcy m3. Dzieląc tę liczbę przez 0,22, otrzymamy powierzchnię lasu, za jaką należało zapłacić podatek. Jest to 19 690 909,09 ha, a to jest w przybliżeniu 2,78 raza więcej niż wynosiła średnia powierzchnia lasów w Lasach Państwowych. Czyli przyrosty te wystarczą na opłacenie niecałych 3 lat podatku leśnego.
Zad. 2. Podatek leśny zostanie obniżony w gminach województwa dolnośląskiego o 0,5 · 0,22 · 186,42 · 0,621 · 591900 ≈ 7537461,88 zł.
Zad. 3. Jeżeli na jednym wykresie umieścimy wysokość dochodów budżetów gmin z tytułu podatku leśnego i średnią cenę drewna, to łatwo zauważymy, że obie krzywe mają podobny kształt, co mogłoby oznaczać, że dochody gmin z tytułu podatku leśnego są uzależnione tylko od średniej ceny drewna. Jednak gdy zbadamy sprawę dokładniej i obliczymy iloraz dochodów i średniej ceny drewna w poszczególnych latach, to widać, że poza rokiem 2012 ten współczynnik rośnie. A to oznacza, że powierzchnia lasów objęta podatkiem leśnym rośnie. Oczywiście nowe nasadzenia, które zwiększają lesistość Polski, nie są opodatkowane, dotyczy to nasadzeń, które zostały wykonane 40 lat temu. Czyli z tych danych na pewno można wywnioskować tylko tyle, że lesistość kraju zwiększała się w przeszłości.
Zad. 1. W 2011 w nadleśnictwie Złotoryja było 17 773,7 ha lasów w klasach powyżej II. Odejmując od tego lasy ochronne i rezerwaty, dostaniemy 4 054,14 ha. Podatek leśny za rok 2011 to 371 324,39 zł, stąd miesięczna rata wynosi 3 043,64 zł.
Zad. 2. Jeśli przyjmiemy powierzchnię administracyjną Polski równą 312 679 km2, to lasy należące do Lasów Państwowych stanowiły w 2006 i 2013 odpowiednio 22,52% i 22,64% powierzchni Polski. W ciągu tych siedmiu lat powierzchnia lasów państwowych wzrosła tylko o 0,51%, a ich zasobność wzrosła aż o 11,81%. Czyli wzrost powierzchni lasów był znacznie wolniejszy od wzrostu zasobności lasów w drewno. W 2013 roku łączna powierzchnia lasów w Polsce wynosiła 29,4% powierzchni kraju, a w ciągu kolejnych siedmiu lat powierzchnia ta powinna wzrosnąć (zgodnie z krajowym programem zwiększenia lesistości) o 2,04%. Ponieważ trudno przewidzieć jak gospodarka leśna wpłynie na zasobność lasów, ma na to wpływ ilość pozyskiwanego drewna, nie możemy jednoznacznie powiedzieć, ile wyniesie lesistość kraju w 2020 roku. Widać też, że w obecnym okresie siedmioletnim lasów musi przybyć czterokrotnie więcej niż przybyło ich w poprzednim siedmioletnim okresie, co może być trudne do wykonania. Jeśli przyjmiemy, że zasobność w 2020 roku pozostanie na poziomie z 2013 roku, czyli wyniesie 257,34 m3/ha, to zasobność wyniesie 2 413,94 mln m3 drewna. Jeśli przyjmiemy, że zasobność będzie wzrastać w tym samym tempie, co poprzednio, to w 2020 roku wyniesie 2 699,03 mln m3 drewna.
Zad. 3. W każdym przykładzie wyjdzie ten sam wynik, czyli ∏/4. Zauważmy, że jeśli w stosie jest n2 wałków drewna (n jest naturalne), każdy o promieniu 1/2n m, to objętość takiego stosu wynosi V = n2·∏·(1/2n)2 = ∏/4 ≈ 0,785 m3. Jeżeli odejmiemy 1 cm na korę, to w 1 mp wyjdzie odpowiednio: 0,754 m3, 0,724 m3, 0,694 m3 i 0,664 m3.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
