luty 2016

luty 2016

Data ostatniej modyfikacji:
2016-10-28

Zad. 1. Jest tam po 20 dwójek, trójek, czwórek, piątek, szóstek, siódemek, ósemek, dziewiątek, ale tylko jedenaście zer. Ile jest jedynek?

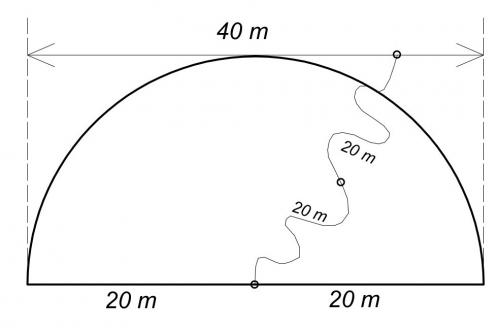
Zad. 2. W jaki sposób, mając do dyspozycji 82 m sznura, sekator, 3 zaciosane drewniane kołki i małą metalową obręcz, można umocować baranka tak, aby pasł się w całym obszarze półkola o promieniu 20 m, ale nie wychodził poza jego obręb?

Zad. 3. Bracia Antek i Bartek zachorowali na grypę. Znudzony leżeniem w łóżku Bartek wymyślił grę w kupki. Z żetonów w jednym z czterech kolorów (zielonych, czerwonych, białych i niebieskich) ułożył cztery stosy po 24 jednakowe żetony w każdym i powiedział do Antka:„Zagrajmy w moją grę. Wygra ten, kto mniejszą liczbą ruchów ułoży z tych żetonów tyle kupek po cztery różne żetony, aby wyczerpać wszystkie możliwości. Pamiętaj, że nie może być dwóch kupek o jednakowym układzie żetonów. Jeden ruch to pobranie dowolnej liczby żetonów z jednego stosu i wyłożenie ich na kupki. Pobranie żetonów z kolejnego stosu, to już kolejny ruch. Ty spróbuj pierwszy.” W ilu ruchach Antek musi ułożyć żetony w kupki, aby mieć pewność, że nie przegra z Bartkiem?

Wyniki:

Spośród lutowych łamigłówek największe trudności sprawiło uczestnikom zadanie 3. Poprawne odpowiedzi podało tylko kilkoro zawodników. Zadanie 1 poprawnie rozwiązali niemal wszyscy, natomiast zadanie 2 - około dwóch trzecich zawodników. W tym zadaniu przyznawaliśmy 1 pkt także za inny niż podany w odpowiedziach sposób wiązania baranka, mianowicie gdy 40-metrowy sznur rozciągnięty był między dwoma kołkami, po sznurze ślizgała się obrączka, a baranek był przywiązany do niej 10-metrowym kawałkiem sznurka i jednocześnie drugim kawałkiem 20-metrowym do trzeciego kołka wbitego w odległości 10 m od środka 40-metrowego sznurka. Nie przyznawaliśmy punktów za odpowiedzi, w których rozpięty sznur pełnił rolę ogrodzenia, gdyż nie stanowił dostatecznej przeszkody dla baranka.

Komplet 3 punktów zdobyli Tomasz Stempniak - uczeń I LO w Ostrowie Wielkopolskim i Dawid Kubicki - student informatyki na UJ.

W Lidze Łamigłówkowej po pięciu miesiącach prowadzą:

I m. - Tomasz Stempniak (15 pkt na 15 możliwych)
II m. - Antoni Buraczewski - uczeń SP 107 we Wrocławiu, Dawid Kubicki, Marcin Kucharski - student matematyki na PWr, Piotr Mazur - urzędnik ze Złotoryi, Wojciech Tomiczek - inżynier z Lipowej (14 pkt)
III m. - Aleksandra Domagała - uczennica Gim. nr 23 we Wrocławiu, Michał Kępiński - uczeń Społecznego LO w Żarach, Krystyna Lisiowska - redaktor z Warszawy, Arnika Piasecka - architekt, a obecnie pracownik samorządowy z Wrocławia, Andrzej Piasecki - administrator IT z Oleśnicy, Jarosław Rybczyński - pracownik naukowy Uniwersytetu Śląskiego (13 pkt)
IV m. - Jacek Bagiński - nauczyciel matematyki z Krakowa, Daria Bumażnik - uczennica II LO w Jeleniej Górze, Bartosz Czyżewski - uczeń I LO w Jeleniej Górze, Krzysztof Danielak - student informatyki przemysłowej na PWr, Franciszek Jan Stepek - uczeń Społecznego Gim. w Żarach, Marzena Wąsiewicz - informatyk a obecnie gospodyni domowa z Kajetan (12 pkt)
V m. - Adrian Szumski - konstruktor z Płocka (11,5 pkt)
VI m. Łukasz Jurasz - uczeń technikum ZSM-E w Żywcu, Jakub Ptak - uczeń SP 64 we Wrocławiu, Adam Stachelek - uczeń SP 301 w Warszawie, Maria Woźny - uczennica Społecznego LO w Żarach (11 pkt).

Wszystkim serdecznie gratulujemy!

Odpowiedzi:

Zad. 1. Jest 21 jedynek wśród liczb od 1 do 100 lub 20 wśród liczb od 2 do 100.

Zad. 2. Przedstawiamy jeden ze sposobów rozwiazania zadania (patrz rysunek). Dzielimy sznur na równe części o długości 41 m. W połowie jednego kawałka sznura wiążemy baranka i jeden koniec tego sznura mocujemy kołkiem w miejscu, które będzie środkiem półkola, a drugi koniec przywiązujemy do obręczy, którą nawlekamy na drugi kawałek sznura rozpiętego na dwóch kołkach równolegle do średnicy półkola i stycznie do półokręgu. Dwumetrowy nadmiar sznurka zużywamy na wiązania lub nadmiar pozostawiamy na końcach.

Zad. 3. Wystarczy 12 ruchów. Muszą powstać 4! = 24 kupki. W przykładowym rozwiązaniu dla kolejnych ruchów podano, z którego stosu bierzemy ile żetonów i na wierzchu których kupek je dokładamy. Na czarno zaznaczone są 4 pierwsze ruchy, na niebiesko 3 następne, na fioletowo 4 dalsze i ostatni na żółto: Z6 (1- 6), C8 (1-2, 7-12), B11 (1, 3-4, 7-8, 13-18), N16 (1-3, 5-7, 9-10, 13-14, 19-24), Z10 (7-9, 11-13, 15-16, 19-20), C11 (3-5, 13-15, 17-19, 21-22), B11 (2, 5-6, 9-11, 19-21, 23-24), Z6 (10, 14, 17, 21-23), N8 (4, 8, 11-12, 15-18), B2 (12, 22), C5 (6, 16, 20, 23-24), Z2 (18, 24).

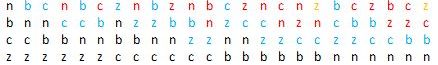
W każdym kolejnym ruchu liczba pobieranych żetonów jest największa, jaką można ułożyć na dotychczasowych kupkach z utrzymaniem zasady, że każda kupka ma inny układu, dlatego mniejszej liczby ruchów być nie może.

Dodaj komentarz

Zadanie 3

Anonimowy (niezweryfikowany), poniedziałek, 01/02/2016 - 12:09

Czy w treści zadania nic nie brakuje?

Odpowiedz

Zad. 3

Joanna Polechońska, poniedziałek, 01/02/2016 - 12:17

W treści zabrakło słowa "cztery". Zadanie jest poprawione.

Odpowiedz

Wątpliwości w zadaniu 2

Niepewny (niezweryfikowany), wtorek, 02/02/2016 - 06:38

Jak rozumieć treść zadania 2? Zdanie "pasł się w obszarze półkola o promieniu 20 m" zobowiązuje do utrzymania zarówno kształtu jak i powierzchni danego obszaru, czy tylko powierzchni? Czy trzeba wykorzystać wszystkie elementy? Czy sznur może być dowolnie cięty, czy ma zostać w całości?

Odpowiedz

Zad. 2

Joanna Polechońska, wtorek, 02/02/2016 - 12:27

Baranek ma mieć możliwość wygryzienia w trawie opisanego w treści półkola i niczego poza nim. Sprzęty "są do dyspozycji". Nie ma obowiązku ich używania. Dopuszczamy cięcie sznura, dlatego dodaliśmy w treści sekator.