Termin przesyłania rozwiązań zostaje przedłużony do 12 VI.
Kluczowym pojęciem w ekonomii jest rynek. Na rynku dochodzi do wymiany towarów i usług oraz do ustalania ich cen na podstawie popytu (ilości towaru, na jaką jest zapotrzebowanie) i podaży (oferowanej ilości towaru). Zamieszczona poniżej tabela na przykładzie jednego produktu przestawia proces dochodzenia do stanu równowagi cenowej.
Popyt (ozn. QD - z ang. quantity demanded) określa, ile towaru konsumenci są skłonni nabyć przy danej jego cenie. Najprostsza metoda ustalenia wielkości popytu na dane dobro na danym rynku polega na zapytaniu potencjalnych konsumentów, ile maksymalnie byliby w stanie zapłacić za dany towar. Prawo popytu stwierdza, że im wyższa jest cena produktu, tym niższe jest na rynku zapotrzebowanie na ten produkt.
Przykład 1. W korporacji Abacus zapytano pracowników, ile zapłaciliby za filiżankę dobrej herbaty w bufecie. Otrzymane odpowiedzi przedstawiono w tabeli.
| konsument | maksymalna cena [zł] |
| Marta | 26 |
| Sylwia | 24 |
| Genowefa | 22 |
| Paweł | 20 |
| Anna | 18 |
| Jacek | 14 |
| Katarzyna | 14 |
| Krzysztof | 12 |
| Mateusz | 10 |
| Rozalia | 10 |
| Milena | 10 |
Uzyskane informacje pozwalają wyznaczyć rynkowy popyt oraz ustalić relację między ceną i zapotrzebowaniem.
| cena rynkowa | zgłaszane zapotrzebowanie |
| 26 | 1 |
| 24 | 2 |
| 22 | 3 |
| 20 | 4 |
| 18 | 5 |
| 14 | 7 |
| 12 | 8 |
| 10 | 11 |
Zaznaczając wielkości z tabeli w układzie współrzędnych, można tę zależność przedstawić graficznie, co pozwala opisać ją matematycznym równaniem. W tym przypadku otrzymane dane dobrze przybliża równanie liniowe, choć nie zawsze musi tak być. Równanie to ma postać QD = 14 – 1/2P, gdzie P oznacza cenę herbaty. Można je też zapisać w postaci odwróconej, przedstawiając cenę w funkcji popytu P = 28 – 2QD.
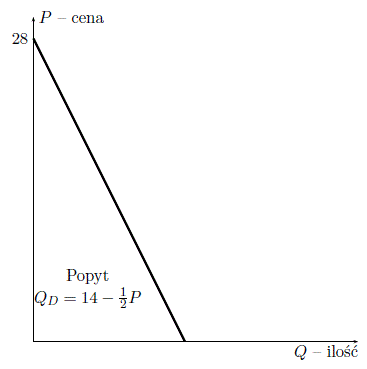
Podaż (ozn. QS - z ang. quantity supplied) określa, ile towaru producenci są skłonni dostarczyć przy danej jego cenie. Podobnie jak w przypadku analizy popytu, można zbadać wpływ ceny towaru na wielkość dostaw. Prawo podaży stwierdza, że im wyższa jest cena produktu, tym więcej tego produktu przedsiębiorcy dostarczają na rynek.
Przykład 2. Do kilkunastu przedsiębiorców wysłano zapytanie ofertowe. Pytano o minimalną cenę, po jakiej mogliby sprzedawać filiżankę dobrej herbaty, gdyby zdecydowali się na dostarczanie jej do bufetu korporacji Abacus. Otrzymane odpowiedzi przedstawiono w tabeli.
| producent | minimalna cena [zł] |
| firma A | 6 |
| firma B | 8 |
| firma C | 8 |
| firma D | 8 |
| firma E | 8 |
| firma F | 8 |
| firma G | 8 |
| firma H | 10 |
| firma I | 10 |
| firma J | 11 |
| firma K | 11 |
| firma L | 13 |
| firma Ł | 13 |
Uzyskane informacje pozwalają wyznaczyć rynkową podaż oraz ustalić relację między ceną a ofertą restauratorów.
| cena rynkowa | liczba zgłaszanych ofert |
| 6 | 1 |
| 8 | 7 |
| 10 | 9 |
| 12 | 13 |
Zaznaczając wielkości z tabeli w układzie współrzędnych, można i tę zależność przedstawić graficznie, co pozwala opisać ją równaniem matematycznym. W tym przypadku również otrzymane dane dobrze przybliża równanie liniowe QS = P – 1, gdzie P oznacza cenę herbaty. Można je zapisać równoważnie w postaci odwróconej, przedstawiając cenę w funkcji podaży P = QS + 1.

Do wyznaczania równań opisujących z najlepszym przybliżeniem krzywe popytu i podaży stosowane są specjalne techniki statystyki matematycznej.
Równowaga rynkowa to stan, w którym zapotrzebowanie na dany towar jest równe wielkości produkcji oferowanej przez wszystkich przedsiębiorców obecnych na rynku.
Przykład 3. Zbierzmy w jednej tabeli dane od konsumentów i dostarczycieli herbaty w korporacji Abacus.
| cena rynkowa | zgłaszane zapotrzebowanie |
oferowany towar |
nadwyżka oferty nad zapotrzebowanie |
| 26 | 1 | 13 | 12 |
| 24 | 2 | 13 | 11 |
| 22 | 3 | 13 | 10 |
| 20 | 4 | 13 | 9 |
| 18 | 5 | 13 | 8 |
| 16 | 5 | 13 | 8 |
| 14 | 7 | 13 | 6 |
| 12 | 8 | 13 | 5 |
| 10 | 9 | 9 | 0 |
| 8 | 11 | 7 | -4 |
| 6 | 11 | 1 | -10 |
Jak wynika z tabeli, ceną zapewniającą równowagę popytu i podaży jest P = 10. Cenę równowagi można też wyznaczyć graficznie.

Można to zrobić także algebraicznie, rozwiązując układ równań: QS = P – 1, QD = 14 –1/2 P, przy czym szukamy takiego P, aby QS = QD. Mamy zatem P – 1 = 14 - 1/2P, skąd P = 10, a QS = 10 – 1 = 9. Stąd wynika, że na lokalny rynek w biurowcu Abacusa dostarczanych będzie 9 filiżanek dobrej herbaty w cenie 10 zł. Żadna inna cena nie byłaby ceną równowagi, np. przy cenie wynoszącej 8 zł producenci chcieliby dostarczać 7 filiżanek herbaty, a konsumenci kupić ich 11. Doprowadziłoby to wkrótce do poniesienia ceny.
Zad. 1. Tabela zawiera dane dotyczące popytu i podaży na kalkulatory kieszonkowe w zależności od ceny.
| cena [zł] | nabywana liczba [tys szt] | oferowana liczba [tys szt] |
| 10 | 9 | 3 |
| 12 | 8 | 4 |
| 14 | 7 | 5 |
| 16 | 6 | 6 |
| 18 | 5 | 7 |
| 20 | 4 | 8 |
Wyznacz krzywe popytu i podaży, naszkicuj je w układzie współrzednych i zaznacz cenę i ilość równowagi.
Zad. 2. Wyznacz cenę równowagi, jeżeli popyt na kawę ziarnistą kształtuje się zgodnie ze wzorem QD = 320 – 5P, a podaż zgodnie ze wzorem QS = 3P.
Zad. 3. Tabela przedstawia popyt i podaż na pizzę Margharita XXL w pewnym miasteczku.
| cena [zł] | zapotrzebowanie konsumentów |
oferta producentów |
| 16 | 135 | 26 |
| 20 | 104 | 53 |
| 24 | 81 | 81 |
| 28 | 68 | 98 |
| 32 | 53 | 110 |
| 36 | 39 | 121 |
Spróbuj przewidzieć, co się stanie na rynku pizzy w tym miasteczku, jeśli cena Margharity XXL zostanie ustalona na 30 zł.
Zad. 1. Dane są równania podaży i poputu na szklanki w pewnej miejscowości: P = 4QS oraz QD = 500–P. Wyznacz cenę równowagi oraz liczbę szklanek na rynku przy stanie rynkowej równowagi.
Zad. 2.Tabela przedstawia liczby ołówków nabywanych przez uczniów i oferowanych przez sprzedawców w Grafitowie.
| cena (zł) | nabywana liczba szt. |
oferowana liczba szt. |
| 1,2 | 0 | 30 |
| 1,0 | 10 | 25 |
| 0,8 | 20 | 20 |
| 0,6 | 30 | 15 |
| 0,4 | 40 | 10 |
| 0,2 | 50 | 5 |
Jaka jest cena równowagi rynkowej? Wyznacz liniowe funkcje popytu i podaży.
Zad. 3. Jaka będzie cena równowagi rynkowej, jeśli przy każdym poziomie ceny sprzedawcy zaoferują o 10 ołówków mniej niż poprzednio?
Zad. 1. W wyniku wzrostu dochodów konsumentów cena równowagi na gałki lodów w pewnym miasteczku podniosła się z 3 zł do 4zł. Wiadomo, że gdyby cena wynosiła 2 zł, wielkość popytu wynosiłaby 2 szt. Pierwotna ilość równowagi wynosiła 1,5 szt, a ostateczna ilość równowagi wynosi 2,5 szt. Wyznacz liniową postać krzywych popytu i podaży.
Zad. 2. W Chlebowie Górnym funkcja popytu na chleb razowy przyjmowała postać QD = 480 - 6P, a funkcja podaży QS = 120 + 3P, gdzie P jest ceną za bochenek. Podczas wakacji przyjechali letnicy popyt wzrósł o 10% przy każdym poziomie ceny. Jaką algebraiczną postać przyjmie nowa funkcja popytu na chleb razowy? Jaka będzie nowa, równoważąca rynek cena i ilość sprzedaży tego chleba?
Zad. 3. W biednej wiosce afrykańskiej funkcja popytu na mąkę ma postać QD = 160–2P, a funkcja podaży QS = 40+P, gdzie P jest ceną za kg mąki w muszelkach. Aby ograniczyć ubóstwo mieszkańców, władca wioski wydał rozporządzenie zabraniające sprzedaży mąki po cenie wyższej niż 30 muszelek. Dla wyeliminowania niedoboru mąki zdecydował się przyznać sprzedawcom subsydium zrównujące popyt z podażą. Ile powinna wynosić dotacja do każdego kg sprzedanej mąki?






 Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było?
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 

