Okrąg Eulera zwany też okręgiem Feuerbacha albo okręgiem dziewięciu punktów jest to jeden z okręgów związanych z trójkątem. Przechodzi on przez dziewięć charakterystycznych punktów dowolnego trójkąta. Okrąg ten zrobił niebywałą karierę w geometrii i stał się bohaterem niezliczonej ilości problemów matematycznych opisujących jego zadziwiające własności. Poniżej uzasadnimy kilka z nich. C.d.n.
Z okręgiem Eulera w tle
Minimaksy w geometrii elementarnej
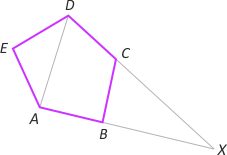Zadania optymalizacyjne, czyli polegające na znajdowanie minimum lub maksimum pewnych zmieniających się wielkości, kojarzą się większości licealistów z użyciem pochodnych. Ale wiele takich zadań można znaleźć także w dziedzinie geometrii elementarnej. Do ich rozwiązania nie są oczywiście potrzebne metody rachunku różniczkowego.
5 komentarzy
Czytaj dalej
Wokół okręgu Eulera
Okrąg Eulera zwany powszechnie okręgiem dziewięciu punktów to jeden z okręgów związanych z trójkątem. Przechodzi on przez dziewięć charakterystycznych punktów dowolnego trójkąta. Okrąg ten zrobił niebywałą karierę w geometrii i stał się bohaterem niezliczonej ilości problemów matematycznych opisujących jego zadziwiające własności. O niektórych pisaliśmy już w artykule Z okręgiem Eulera w tle. Teraz poznamy kolejne.
Punkty szczególne trójkąta
Wiadomo, że każdy trójkąt ma kilka środków, np. środek ciężkości, środek okręgu opisanego, środek okręgu wpisanego, punkt przecięcia prostych zawierających wysokości (tzw. ortocentrum trójkąta). Ale punktów szczególnych trójkąta jest znacznie więcej. Opowiemy o nich przy innej okazji. W tym artykule za punkty szczególne (oprócz wyżej wymienionych) uznamy jeszcze środki okręgów dopisanych do trójkąta.
Twierdzenie Ptolemeusza
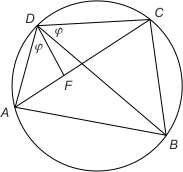Twierdzenie Ptolemeusza opisuje zależność między bokami a przekątnymi czworokąta wpisanego w okrąg. Orzeka, że iloczyn długości tych przekątnych jest równy sumie iloczynów długości przeciwległych boków tego czworokąta. Jest też prawdziwe twierdzenie odwrotne. Odkrycie tych twierdzeń i przeprowadzenie ich dowodów przypisuje się Klaudiuszowi Ptolemeuszowi (100-168) - greckiemu astronomowi, matematykowi i geografowi.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
