Na zakończenie roku 2013 ogłaszamy konkurs dla kółek matematycznych w szkołach, klas, dla rodzin, a także dla pojedynczych uczniów, nauczycieli i pasjonatów matematyki. Wstawiając znaki działań i operacji oraz nawiasy pomiędzy cyfry numeru roku 2013, należy otrzymać kolejne liczby naturalne od 1 do jak największej. Nie może być między nimi żadnej luki. Dla rekordzistów przewidziano nagrody. Czas na przesyłania rozwiązań jest - rzecz jasna - do końca roku.
Konkurs Roku 2013
9 komentarzy
Czytaj dalej
Aquapark 'Kaskady 2'
Zadania o napełnianiu basenów jeszcze nie tak dawno były zmorą niejednej lekcji matematyki. Spróbuj swoich sił w unowocześnionej wersji podobnych zadań. W tym tekście (podobnie jak w Aquaparku 'Kaskady 1') proponujemy rozwiązanie kilku zadań. Tym razem wymagają one większej wprawy rachunkowej, więc radzimy zacząć od tych z poprzedniego artykułu.
Aquapark 'Kaskady 1'
Zadania o napełnianiu basenów jeszcze nie tak dawno były zmorą niejednej lekcji matematyki. Spróbuj swoich sił w unowocześnionej wersji podobnych zadań.
Wypukłe wielościany w sześcianie
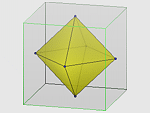Rzecz będzie się działa w sześcianie. Dla różnych kolekcji K wyróżnionych punktów sześcianu będziemy oglądali W = W(K) = najmniejszy wypukły wielościan zawierający punkty z K. Na prostych zadaniach możesz przetestować swoją wyobraźnię przestrzenną. Spróbuj.
Wypukłe wielościany w graniastosłupie
Rzecz będzie się działa w graniastosłupie prawidłowym o podstawie sześciokąta. Dla różnych kolekcji K wyróżnionych punktów graniastosłupa będziemy oglądali W = W(K) = najmniejszy wypukły wielościan zawierający punkty z kolekcji K. Na prostych zadaniach możesz przetestować swoją wyobraźnię przestrzenną. Spróbuj.
