Tegoroczna noc sylwestrowa była na całym świecie o sekundę dłuższa. Korekta miała na celu dostosowanie czasu zegarowego do rzeczywistego tempa ruchu obrotowego Ziemi, która jest spowalniana oddziaływaniem grawitacyjnym innych planet. Taką "sekundę przestępną" dodaje się dość nieregularnie, średnio raz na kilka lat.
Rok 2008 był dłuższy o sekundę
Jak wygląda $\color{red} \sqrt{x^2-1}$ ?
Przed przeczytaniem zrób test: naszkicuj w 20 sekund wykres funkcji
Przychodzi funkcja $\color{red}\sqrt{x^2-1}$ do lekarza
Przychodzi funkcja do lekarza, no bo dokąd ma pójść, jeśli chce, aby ktoś ją zbadał? Dokuczają jej kłopoty z... trawieniem i nawracające kłucie w dołku. Czy pan doktor będzie umiał tym dolegliwościom zaradzić?
Wykresy z oddali
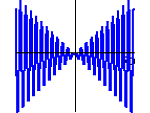Co widać, gdy będziemy oddalali się od wykresu funkcji dalej i dalej, i dalej...? Co widać, gdy jednostki, jednakowe na obu osiach, będą wyglądały na coraz mniejsze? Możesz to po prostu zobaczyć. Lepiej jednak najpierw... pomyśleć. Zawsze też można sprawić sobie własny wykres. Pamiętaj jednak, że chcemy 'zobaczyć' nie konkretny wykres, lecz to, co z niego 'pozostaje w umyśle', gdy 'oddalimy się w nieskończoność'.
Zoom, zoom, zoom... i twierdzenia
Działanie operatora Hatchinsona można obejrzeć w poprzednim tekście na ten temat
(tutaj zakładamy, że Czytelnik obejrzał i zrozumiał wiele przykładów działania takich operatorów).
Teraz zastanowimy się nad tym 'co widać dalej'.
Co widać nie na obrazkach, ale poza nimi, co widać 'w nieskończoności'.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
