 Jeśli można wymyślać (zmyślać) rowery o kwadratowych 'kołach' (tak jak robiliśmy to we wcześniejszych tekstach: Rolling Stones (2) - Polygon Rover oraz Rolling Stones (3) - Rysują cykloidę - zajrzyj tam koniecznie), to może można wymyślać też drogi, po których tymi rowerami będzie się jeździć jak po stole?
Spróbujmy!
Jeśli można wymyślać (zmyślać) rowery o kwadratowych 'kołach' (tak jak robiliśmy to we wcześniejszych tekstach: Rolling Stones (2) - Polygon Rover oraz Rolling Stones (3) - Rysują cykloidę - zajrzyj tam koniecznie), to może można wymyślać też drogi, po których tymi rowerami będzie się jeździć jak po stole?
Spróbujmy!
Rolling Stones (4) - Matematyczne wyboje
Rolling Stones (4) - Matematyczne wyboje
 Jeśli można wymyślać (zmyślać) rowery o kwadratowych 'kołach' (tak jak robiliśmy to we wcześniejszych tekstach: Rolling Stones (2) - Polygon Rover oraz Rolling Stones (3) - Rysują cykloidę - zajrzyj tam koniecznie), to może można wymyślać też drogi, po których tymi rowerami będzie się jeździć jak po stole?
Spróbujmy!
Jeśli można wymyślać (zmyślać) rowery o kwadratowych 'kołach' (tak jak robiliśmy to we wcześniejszych tekstach: Rolling Stones (2) - Polygon Rover oraz Rolling Stones (3) - Rysują cykloidę - zajrzyj tam koniecznie), to może można wymyślać też drogi, po których tymi rowerami będzie się jeździć jak po stole?
Spróbujmy!
Czy istnieje wzór na n-tą liczbę pierwszą?
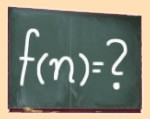 To pytanie nie jest jednoznaczne, bo...
To pytanie nie jest jednoznaczne, bo...
nie wiadomo co to znaczy 'wzór' i nie
wiadomo co to znaczy 'istnieje'.
Ale w ogóle co to za pytanie 'czy istnieje'? Niemal w każdym programie do obliczeń symbolicznych (CAS)
istnieje funkcja podająca n-tą liczbę pierwszą (np. w MAPLEu jest
ithprime(n) ). Z drugiej jednak strony szyfry, które kodują nasze
dane w internecie, bazują na kłopotach z rozkładem liczb na czynniki pierwsze,
więc gdyby taka funkcja istniała...
Czy istnieje wzór na n-tą liczbę pierwszą?
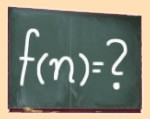 To pytanie nie jest jednoznaczne, bo...
To pytanie nie jest jednoznaczne, bo...
nie wiadomo co to znaczy 'wzór' i nie
wiadomo co to znaczy 'istnieje'.
Ale w ogóle co to za pytanie 'czy istnieje'? Niemal w każdym programie do obliczeń symbolicznych (CAS)
istnieje funkcja podająca n-tą liczbę pierwszą (np. w MAPLEu jest
ithprime(n) ). Z drugiej jednak strony szyfry, które kodują nasze
dane w internecie, bazują na kłopotach z rozkładem liczb na czynniki pierwsze,
więc gdyby taka funkcja istniała...
Rolling Stones (3) - Rysują cykloidę
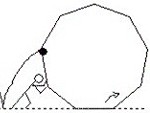 Toczymy po prostej n-kąt foremny. Zbadajmy, jaką trajektorię kreśli ustalony wierzchołek.
Toczymy po prostej n-kąt foremny. Zbadajmy, jaką trajektorię kreśli ustalony wierzchołek.






 Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było?
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 

