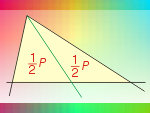
Środkowa trójkąta, czyli odcinek łączący wierzchołek ze środkiem przeciwległego boku, dzieli pole tego trójkąta na połowy. Są też inne odcinki dzielące trójkąt na dwie figury o równych polach.
Jak wygląda kolekcja wszystkich takich odcinków? Pomyśl i zobacz!
Wszystkie połowiące pole trójkąta
Domino - jak leci
O tym, jak leży domino po upadku, pisaliśmy w tekście Domino - jak leży. Ale jak upada domino? Warto się nad tym spokojnie zastanowić przed przeczytaniem niniejszego artykułu. Można nawet wykonać kilka eksperymentów. Zamiast kamieni domina można wykorzystać pudełka od zapałek.
Siła wektorów i liczydła
Gdyby Newton miał takie liczydło, jakim jest arkusz kalkulacyjny,
pewnie nie stworzyłby rachunku różniczkowego i całkowego. Dzięki wektorom i za pomocą takiego liczydła, można zobaczyć, jak spada jabłko, nawet uwzględniając opory powietrza. Newton nie mógł, ale Ty zobacz koniecznie! Zajrzyj też do tekstu Siła wektorów (i geometrii).
Symetryzacja Steinera
Najprostsze własności symetryzacji Steinera są zebrane w dwóch kolekcjach zadań:
Symetryzacja na kratkach
i Symetryzacja na gładko. Warto najpierw zrobić choćby tylko kilka z nich. Tu pokażemy, że te własności są spełnione nie tylko dla konkretnych trójkątów, czy czworokątów. Pokażemy, że zamiast rachunków wystarczą pewne ogólne obserwacje geometryczne.
Rozproszenie i koszty transportu
Zamiast o punktach i figurach w artykule mowa jest o oddziałach fabryki, rozproszeniu i kosztach transportu. Brzmi to jak temat z zakresu ekonomii, a tymczasem to prosta matematyka. Zobacz sam.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
