Fundacja Matematyków Wrocławskich
Instytut Matematyczny Uniwersytetu Wrocławskiego
pl. Grunwaldzki 2/4, 50-384 Wrocław
zgłoszenia za pomocą formularza on-line do 15 XI I 2024
symulacja dla nauczycieli: 16 XI 2024 Polanica-Zdrój
oraz IM UWr Wrocław: SP 19 XI, LO 26 XI godz. 17:00 s. 601
eliminacje szkolne: SP 22 XI 2023, LO 29 XI 2024
odsyłanie wyników: SP 28 XI 2024, LO 5 XII 2024
ogłoszenie listy finalistów: 30 XI 2024, 7 XII 2024
finał: SP 7 XII 2024, LO 14 XII 2024
Konkurs ma niespotykaną formę - czysto akademicką. Polega na wysłuchaniu wykładu, a następnie rozwiązywaniu zadań dotyczących wyłożonego materiału. Nie korzysta z wcześniejszej wiedzy, dzięki czemu jest adresowany nie tylko do najlepszych matematyków, ale do wszystkich uczniów o dużym potencjale intelektualnym. Ważna jest w nim umiejętność słuchania i przetwarzania informacji. Dużą trudność stanowi (zwłaszcza dla młodszych uczniów) sensowne robienie notatek i posługiwanie się nimi. Wykłady eliminacyjne prowadzą nauczyciele w szkołach. Wykłady finałowe prowadzą pracownicy, doktoranci lub studenci Instytutu Matematycznego UWr. Zazwyczaj dotyczą one tego samego zagadnienia dla wszystkich poziomów edukacyjnych, co czyni niezwykle ciekawą analizę publikowanych w Internecie wyników.
W latach 2001-2003 konkurs odbywał się w tradycyjnej formie - rozwiązywania zadań. Składał się z dwóch etapów: Prologu (rozgrywanego w szkołach) i Finiszu (w Instytucie Matematycznym UWr). Do Finiszu przechodziło 4 najlepszych uczniów z każdej szkoły. Po godzinie od zakończenia konkursu ogłaszane były wyniki, a czas oczekiwania na nie wypełniał poczęstunek, warsztaty i wykłady popularnonaukowe. Organizatorami zawodów byli nauczyciele z wrocławskich szkół: Stanisława Grzywna, Roman Lamch, Zbigniew Lorkiewicz, Józef Łoziński, Ewa Mordel i Krzysztof Omiljanowski z IM UWr.
W obecnej formie KOMA organizowana jest od 2005 r. Autorką wykładów i zadań eliminacyjnych jest Małgorzata Mikołajczyk, a wykładów i zadań finałowych - Krzysztof Omiljanowski (2005-2017) i Małgorzata Mikołajczyk (od 2018). W roku 2018 zadania eliminacyjne przygotował Tomasz Drab, a pomysł ten stanowił podstawę jego rozprawy doktorskiej.
Od 2022 roku konkurs dla Juniorów jest umieszczony na liście kuratoryjnej i daje punkty rekrutacyjne przy ubieganiu się o przyjęcie do szkoły średniej.
Tematy wykładów eliminacyjnych i finałowych z poszczególnych lat:
- I edycja - 2005
eliminacje: SP - Systemy liczbowe, GM - Liczby wymierne i niewymierne, LO - Składanie przekształceń,
finały: Permutacje - II edycja - 2006
eliminacje: SP - Równania, GM - Rozwiązywanie równań, LO - Zmienne i parametry,
finały: Różnica symetryczna (wykład, zadania) - III edycja - 2007
eliminacje: SP - Kąty wpisane i dopisane, GM i LO - Kąty i odcinki na okręgach,
finały: Rozproszenie zbiorów (wykład, zadania) - IV edycja - 2008
eliminacje: SP - Odcinki i okręgi, GM - Logarytmowanie, LO - Liczby zespolone
finały: Kropkoland - V edycja - 2009
eliminacje: SP, GM, LO - Silnie i słabnie
finały: Symetryzacja Steinera (wykład i zadania) - VI edycja - 2010
eliminacje: SP - Trójkąt Pascala, GM - Dwumian Newtona, LO - Średnie
finały - Wierzchołki piramid (wykład i zadania) - VII edycja - 2011
eliminacje: SP - Potęgowanie, GM i LO - Cechy podzielności
finały - Piramidy (wykład i zadania, ciąg dalszy) - VIII edycja - 2012
eliminacje: SP i GM - Postęp arytmetyczny, LO - Rozkład normalny
finały - Środki morfoz (wykład i zadania, ciąg dalszy) - IX edycja - 2013
eliminacje SP, GM, LO - Wielokąty foremne
finały - Wielociągi (wykład i zadania, ciąg dalszy) - X edycja 2014
eliminacje: SP - Parkiety z wielokątów, GM, LO - Macierze
finały - Nieziemskie przyciąganie (wykład i zadania) - XI edycja 2015
eliminacje: SP, GM, LO - Logika boolowska
finały - Namioty (wykład i zadania) - XII edycja 2016
eliminacje: SP, GM, LO - River crossing (wykład i zadania)
finały - Hydrologia (wykład i zadania) - IIIX edycja 2017
eliminacje: SP, GM, LO - Permutacje
finały: Równanie figur - XIV edycja 2018
eliminacje: SP, GM, LO - Rachunek lambda
finały: Pola i obwody - XV edycja 2020/2021
eliminacje: SP - Trygonometria, LO - Relacje równoważności (wykłady i zadania)
finały: SP - Kombinatoryka, LO - Stars & Stripes (wykłady i zadania) - XVI edycja 2021/2022
eliminacje: SP - Równania kwadratowe, LO - Nierówności (zadania)
finały: SP - Kąty w wielokątach, LO - Równania funkcyjne (wykłady i zadania) - XVII edycja 2022
eliminacje SP, LO: Krótkie zapisy dużych liczb
finały SP, LO: Nieskończoności - XVIII edycja 2023
eliminacje: SP - Odległość na osi, LO - Logika indukcji
finały SP, LO: Ułamki Fareya - XIX edycja 2024
eliminacje: SP, LO
finały SP, LO:
Zwycięzcy KOMY z kolejnych lat w poszczególnych kategoriach:
- I - 2005
SP 12 Wrocław - Szymon Hendrich
GIM 49 Wrocław - Karol Konaszyński
LO III Kalisz - Przemysław Piotrowski
- II - 2006
SP 12 Wrocław - Kacper Pawlak
GIM 1 Wrocław - Monika Sikora
LO XIV Wrocław - Karol Konaszyński - III - 2007
SP 76 Wrocław - Mateusz Piskorski
GIM 49 Wrocław - Mateusz Gołębiewski
LO III Wrocław - Dorota Moskal - IV - 2008
SP 26 Wrocław - Anna Biadasiewicz
GIM 49 Wrocław - Maciej Dulęba
LO III Wrocław - Mateusz Sieradzan i Marcin Słowik - V - 2009
SP 28 Wałbrzych - Filip Barański
GIM 29 Wrocław - Tomasz Drab
LO V Wrocław - Balthasar Szczepański - VI - 2010
SP 107 Wrocław - Dawid Ptak
GIM 49 Wrocław - Michał Hadryś
LO XIV Wrocław - Mateusz Gołębiewski - VII - 2011
SP 24 Wrocław - Dawid Ignasiak
GIM 1 Wrocław - Grzegorz Ciesielski
LO I Jelenia Góra - Mateusz Skórski - VIII - 2012
SP 76 Wrocław - Radosław Girul
GM 10 Wrocław - Barbara Zięba
LO III Wrocław - Tomasz Drab - IX - 2013
SP 3 Wrocław - Stanisław Łyczkowski, SP 76 Wrocław - Mateusz Padarz
GM 14 Wrocław - Jakub Kamiński
LO III Wrocław - Michał Żłobicki - X - 2014
SP 53 Wrocław - Łukasz Orski
GM 26 Wrocław - Iwo Pilecki-Silva
LO III Wrocław - Michał Żłobicki - XI - 2015
SP 3 Wrocław - Bartłomiej Bychawski
GM 49 Wrocław - Jakub Famulski, GM 14 Wrocław - Jakub Kamiński, GM Łużyckie Zgorzelec - Olimpia Pozauć
LO III Wrocław - Grzegorz Ciesielski i Barbara Zięba, LO 14 Wrocław - Arkadiusz Kozdra - XII - 2016
SP 107 Wrocław - Antoni Buraczewski
GM Oxpress Bolesławiec - Oliwia Sas, GM 5 Głogów - Michał Rzepka, GA PWr - Krzysztof Gąciarz i Mateusz Padarz
LO 3 Wrocław - Maciej Korpalski - IIIX - 2017
SP 6 Kłodzko - Hanna Kuriata
GA PWr Wrocław - Łukasz Orski
III LO Wroław - Dawid Ignasiak - XIV - 2018
SP 24 Wrocław - Paulina Żeleźnik
GA PWr Wrocław - Grzegorz Ciepłucha
LO 3 Wrocław - Krzysztof Olejniczak - XV - 2020/2021
Młodzicy - Filip Pawicki MdM IM UWr
Juniorzy - Mateusz Wawrzyniak SP Atut Wrocław
Licealiści - Cyprian Ziółkowski LO14 Wrocław - XVI - 2021/2022
Młodzicy - Miłosz Popowicz MKM MdM IM UWr
Juniorzy - Aleksander Porębny MKM OMJ IM UWr
Licealiści - Jakub Rudzik ALO PWr - XVII - 2022
Młodzicy - Karol Kulczycki KM Mały Pitagoras
Juniorzy - Monika Izworska SP 3 Wrocław
Licealiści -Jan Pezda III LO Wrocław - XVIII - 2023
Młodzicy - Antoni Lange SP 1 Wrocław
Juniorzy - Artur Brzeziński SP 9 Wrocław
Licealiści - Łukasz Ganczarek LO 3 Wrocław - XIX- 2024
W obu etapach uczniowie wysłuchują ok. godzinnego wykładu z matematyki, a potem przez 60 minut rozwiązują zadania dotyczące tego samego tematu. Mogą korzystać ze zrobionych podczas wykładu notatek. W finałach temat nie jest związany z programem matematyki szkolnej.
Eliminacje. Odbywają się w szkole, wykład wygłasza nauczyciel. Temat wykładu związany jest z programem nauczania, ale szeroko poza niego wykracza. Treść wykładu i zadania omawiane są wcześniej na spotkaniu nauczycieli podczas symulacji. Szkoły spoza Wrocławia mogą otrzymać notatki do wykładu i zadania pocztą. Wskazane jest zrobienie jednodniowej przerwy między wykładem a rozwiązywaniem zadań. Zadania sprawdza nauczyciel i przesyła organizatorom wyniki najlepszych 10 osób oraz prace do weryfikacji. Zwrotnym e-mailem otrzymuje informację, kto zakwalifikował się do finału. Do finału wchodzą wszyscy uczniowie, którzy przekroczyli określony próg punktów lub 3 najlepsze osoby z każdej szkoły.
Finały. Odbywają się w Instytucie Matematycznym UWr. Po wykładzie następuje 40-minutowa przerwa na przejrzenie i uporządkowanie notatek, dyskusję z wykładowcą, kolegami i nauczycielami. Po części zadaniowej następuje dalsza część wykładu, dotycząca zastosowań poznanego pojęcia. W tym czasie jury ocenia prace i wyłania zwycięzców.
ETAP SZKOLNY
Temat wykładu: Liczby wymierne i niewymierne
Treść wykładu: Definicje i własności liczb wymiernych i niewymiernych, dowody niewymierności.
1. Zakreśl właściwą odpowiedź.
Suma dwóch liczb wymiernych jest:
a) wymierna b) niewymierna c) dowolna
Suma dwóch liczb niewymiernych jest:
a) wymierna b) niewymierna c) dowolna
Suma liczby wymiernej i niewymiernej jest:
a) wymierna b) niewymierna c) dowolna
Iloczyn dwóch liczb wymiernych jest:
a) wymierny b) niewymierny c) dowolny
Iloczyn dwóch liczb niewymiernych jest:
a) wymierny b) niewymierny c) dowolny
Iloczyn liczby wymiernej i niewymiernej jest:
a) wymierny b) niewymierny c) dowolny
2. Wskaż liczbę wymierną i niewymierną leżącą pomiędzy:
a) √2 i √3
b) 3,1415 i π
c) -1/6 i -1/7
d) a i a+10-6, gdzie a jest liczbą wymierną.
3. Udowodnij niewymierność √6.
ETAP FINAŁOWY
Temat wykładu: Kropkoland
Treść wykładu: Aksjomaty prowadzenia prostych prostopadłych i równoległych na punktach kratowych, powiększanie figur w skali, obracanie kątów
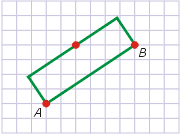
1. Narysuj trójkąt ostrokątny o podstawie AB i polu równym polu danego prostokąta.
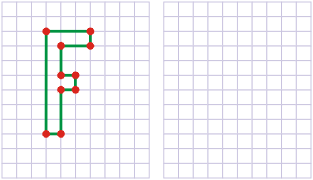
2. Narysuj figurę o wierzchołkach w punktach kratowych, o tym samym kształcie, co figura F, ale o dwukrotnie większym polu.
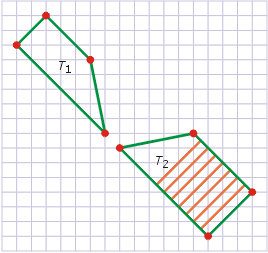
3. Zaznacz, wzdłuż której linii uciąć trapez T2, aby miał pole równe polu trapezu T1.
Fotoreportaż z X edycji konkursu matematycznego KoMa
zdjęcia: Wojciech Obremski
Fotoreportaż z IIIX edycji konkursu matematycznego KoMa
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
KOMA w SP
Prezentacja do wykładu - świetna. Uczniowie mówili, że dużo zrozumieli i dużo się nauczyli. Świetną zabawą było zapisywanie kodów parkietów oraz rozpoznawanie rodzajów parkietów. Wierzchołki prawidłowe i nieprawidłowe zrozumieli szybciej niż ja, kiedy przygotowywałam się do wykładu :). Wieczorem część uczniów próbowała znaleźć "coś" podobnego w internecie, ale nie było tego zbyt dużo :) Według uczniów było za mało czasu na wykładzie, aby przećwiczyć
parkiety dualne, nieforemne tylko "liznęliśmy", rozetowy, niecykliczny oraz z ornamentem tylko pokazałam i podałam definicję. Większości dzieci pozostał niedosyt i chciały więcej. Zbyt mało czasu było na zadania. Rzadko kto zdążył narysować parkiety, choć wszyscy twierdzili, że daliby radę, gdyby mieli więcej czasu. Akurat w klasach V i VI robimy klasyfikację czworokątów. Dzieci z
satysfakcją już po konkursie przy podawaniu własności czworokątów mówiły, że kwadrat jest figurą foremną a prostokąt nie. Dla mnie konkurs - super! Świetna zabawa dla nauczyciela i dla dzieci. Bardzo dziękuję za przygotowanie konkursu! Chłopiec, który napisał go najlepiej w szkole, powiedział, że w życiu nie pisał trudniejszego konkursu. Tego samego zdania byli też inni uczestnicy.
Zadania komowe
Zadań na Komie jest zawsze dużo (za dużo) i nie da się zrobić wszystkiego. Każdy uczeń może wybrać to, co zrozumiał z wykładu najlepiej. Nie trzeba zrobić wszystkiego. Poprawne rozwiązanie około połowy zadań zazwyczaj wystarcza, aby wejść do finału. Materiału do niektórych zadań celowo nie ma w części wykładowej - to są zadania dla najlepszych. Rysowanie parkietów było wypełniaczem czasu dla najsłabszych uczniów, którzy nie poradzili sobie z zadaniami - mogli się wtedy wykazać rysunkami. Te wszystkie aspekty części zadaniowej są zawsze wcześniej omawiane na seminarium dla nauczycieli, więc nauczyciel może właściwie ukierunkować pracę uczniów podczas konkursu.
Chciałem powiedzieć
Chciałem powiedzieć, że wykład prowadzony przez panią Agatę bardzo mi się nie podobał. Ta pani nie tafiła ani do mnie, ani do moich kolegów. Zawsze biorę udział w matematycznych konkursach FMW i jeżdżę na obozy. Inne panie fajnie prowadzą zajęcia. Pani Agata nie za bardzo umie tłumaczyć. Może nadałaby się do przedszkola, a i tak nie wiem, czy przedszkolaki byłyby zadowolone. Porażka w tym roku!
O proszę
Widzę komentarz sfrustrowanego gimnazjalisty, który porusza temat, który mnie też nurtował. Wyjaśnijmy: byłem w tym roku na dwóch wykładach tym dla gimnazjum i tym dla liceum (dla gim, bo mam kuzyna, który brał udział). Faktycznie zgodzę się. Moim zdaniem wykład pani Agaty był kiepski. Chyba sam lepiej bym go poprowadził. Już mówię dlaczego. Pani Agata była strasznie zdenerwowana. Cała sala ludzi - rozumiem, Ale mówiła nieskładnie i niespójnie. Może i wie, co chce powiedzieć, ale kompletnie nie umie. Czy nie mogliście dać kogoś, kto ma większe obycie w prowadzeniu zajęć? Nie obrażając pani Agaty, no niestety nie umie prowadzić zajęć. Mam nadzieję, że zostało jej jeszcze kilka lat studiów i zdąży się czegoś nauczyć, bo takiego nauczyciela bym nie chciał mieć.
Buractwo!
Ja też byłem w zeszłym roku na gimnazjalnej Komie. Temat wykładu był bardzo fajny i całkiem składnie opowiedziany. Można było nauczyć się wszystkiego, co potrzebne było do rozwiązania zadań. Powyżej wypowiedział się jakiś łom z Czternastki (kto normalny podpisałby się 'uczeń 14LO'?) i zapewne jego gimnazjalny kuzynek (wpisy pojawiły się 2 miesiace po Komie i dziwnym zbiegiem okoliczności, tego samego dnia). Przede wszystkim, gościu, jesteś oszustem. Po co lazłeś tydzień wcześniej na wykład? Parcie na sukces za wszelka cenę? Tego was uczą w tej szkole? Oszukiwanie honorowe nie jest, a publiczne przyznawanie się do oszustwa, to już buractwo. Ale chyba nie wyszedłeś na tym najlepiej, bo Czternastka w zeszłorocznej Komie raczej poległa.
KOMA 2016
Bardzo dziękujemy za ciekawy i wspaniale przeprowadzony konkurs dla gimnazjalistów. Uczniowie mieli okazję przeżyć kolejną fantastyczną matematyczną przygodę. Bardzo pozytywnie ocenili tegoroczny finał i towarzyszącą mu miłą atmosferę.
Wykład 2016
Moim uczniom z GM także bardzo podobał się tegoroczny wykład komowy.