W tej chwili stronę przegląda
10 użytkowników online.
Logowanie dla redaktorów
STATYSTYKA MIESIĄCA
MARZEC
Nowe artykuły - 29
Unikalne wizyty - 98 489
Odsłony - 2 550 116
LUTY
Nowe artykuły - 31
Unikalne wizyty - 102 941
Odsłony - 2 331 138
STYCZEŃ
Nowe artykuły - 36
Unikalne wizyty - 103 585
Odsłony - 2 645 180
GRUDZIEŃ
Nowe artykuły - 28
Unikalne wizyty - 116 421
Odsłony - 2 174 934
LISTOPAD
Nowe artykuły - 34
Unikalne wizyty - 174 535
Odsłony - 2 865 087
PAŹDZIERNIK
Nowe artykuły - 44
Unikalne wizyty - 144 993
Odsłony - 2 800 600
WRZESIEŃ
Nowe artykuły - 28
Unikalne wizyty - 86 948
Odsłony - 2 219 604
SIERPIEŃ
Nowe artykuły - 29
Unikalne wizyty - 61 309
Odsłony - 1 406 565
LIPIEC
Nowe artykuły - 44
Unikalne wizyty - 69 906
Odsłony - 1 838 382
CZERWIEC
Nowe artykuły - 34
Unikalne wizyty - 73 965
Odsłony - 2 280 853
MAJ
Nowe artykuły - 30
Unikalne wizyty - 97 567
Odsłony - 3 586 757
KWIECIEŃ
Nowe artykuły - 31
Unikalne wizyty - 96 169
Odsłony - 3 257 155
Funkcja słonia na lekcjach matematyki jest nie do przecenienia.
Słoń zrazu może zasłaniać - stawiać pytania, by potem odsłaniać - wyjaśniać. Każdy nauczyciel to wie...
Tu zajmiemy się jednym konkretnym zagadnieniem:
czy na podstawie częściowo zasłoniętego wykresu
można rozpoznać funkcję. Układający zadania na tegoroczną maturę niestety nie postawili sobie takiego pytania, a szkoda.
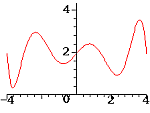Wydaje się, że wierzchołek (maksimum lokalne funkcji),
to taki punkt, z którego będzie się schodzić, w którąkolwiek stronę pójdziemy
(tzn. funkcja jest rosnąca na pewnym przedziale 'na lewo' od spodka wysokości poprowadzonej z wierzchołka i
malejąca na pewnym przedziale 'na prawo' od tego spodka).
Czy tak jest, czy tylko się wydaje?
Jeśli można wymyślać (zmyślać) rowery o kwadratowych 'kołach' (tak jak robiliśmy to we wcześniejszych tekstach: Rolling Stones (2) - Polygon Rover oraz Rolling Stones (3) - Rysują cykloidę - zajrzyj tam koniecznie), to może można wymyślać też drogi, po których tymi rowerami będzie się jeździć jak po stole?
Spróbujmy!
Do 20 IV w galerii "Pod Hugonem" w IM UWr można wziąć udział w plebiscycie publiczności na najlepszy model w konkursie matematycznego origami "Żuraw 2024".
Bez wątpienia, prawdziwa tych kształtów forma istnieje wiekuiście w umyśle Boga-Stwórcy.
Johannes Kepler
W kwietniu odbędzie się finał LXXV Olimpiady Matematycznej, a zaraz po nim finał XXII Olimpiady Lingwistyki Matematycznej. W pierwszym wystartuje 16, a w drugim 6 uczniów z wrocławskich liceów.
Nagrodę FMW im. Kamila Duszenki za rok 2024 otrzymała Lei Chen z Uniwersytetu Maryland. Studiowała matematykę na Uniwersytecie w Pekinie, doktorat pod kierownictwem Bensona Farba obroniła na Uniwersytecie w Chicago. Jest autorką pionierskich prac na temat struktury grup klas odwzorowań powierzchnii. Jej hobby to śpiewanie, snowboard i tenis.
Ile co najmniej ścian musi mieć wielościan, by był topologicznie torusem? W roku 1977 węgierski matematyk Lajos Szilassi [wym. lojosz siloszszi] podał przykład takiego wielościanu mającego tylko 7 ścian. Są one wklęsłymi 6-kątami i każda graniczy z każdą inną.
Czy istnieje inny wielościan niż powyższy, którą ma tę własność, że każda jego ściana graniczy z każdą inną?
Czy znane od wieków domino może stanowić łamigłówkowe wyzwanie? W wersji graficznej jak najbardziej. Dominograf - stosując klasyczne kamienie i zasady gry w domino, ułóż krzyż (jak na rysunku). W tej wersji ostatni kamień nie pasuje. Zacznij od nowa. Nagrodzimy pięć osób, które jako pierwsze przyślą zdjęcie rozwiązania na adres mikolaj@math.uni.wroc.pl .
