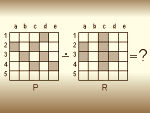
 Co to jest różnica symetryczna? Nie wiesz? Nigdy nie słyszałeś o tym w szkole? A może słyszałeś, ale dokładnie już nie pamiętasz? Zrób dziewięć zadań i będziesz wiedział!
Co to jest różnica symetryczna? Nie wiesz? Nigdy nie słyszałeś o tym w szkole? A może słyszałeś, ale dokładnie już nie pamiętasz? Zrób dziewięć zadań i będziesz wiedział!
Kółko matematyczne
Różnica symetryczna (w zadaniach)
Domino - wąż paton
 Samotny jesienny wieczór. Nie masz z kim pogadać, ani rozegrać partyjki domina. Nie martw się! Możesz spokojnie porozmyślać, zastanowić się, na przykład nad pytaniem: czy w grze w domino możliwe są partie remisowe.
Samotny jesienny wieczór. Nie masz z kim pogadać, ani rozegrać partyjki domina. Nie martw się! Możesz spokojnie porozmyślać, zastanowić się, na przykład nad pytaniem: czy w grze w domino możliwe są partie remisowe.
W labiryncie
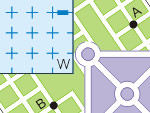 Wśród łamigłówek logicznych często pojawiają się rozmaite zadania labiryntowe. Nie wymagają one właściwie żadnej specjalistycznej wiedzy matematycznej, jedynie spostrzegawczości, wyobraźni, czasem biegłości rachunkowej i odrobiny wprawy. Znakomicie nadają się na kółko matematyczne lub zajęcia na zielonej szkole.
Wśród łamigłówek logicznych często pojawiają się rozmaite zadania labiryntowe. Nie wymagają one właściwie żadnej specjalistycznej wiedzy matematycznej, jedynie spostrzegawczości, wyobraźni, czasem biegłości rachunkowej i odrobiny wprawy. Znakomicie nadają się na kółko matematyczne lub zajęcia na zielonej szkole.
Podziel działkę
 Zadania o podziale figur na mniejsze, przystające części, przy ewentualnym zachowaniu pewnych dodatkowych warunków, często występują wśród łamigłówek matematycznych. Nie wymagają na ogół żadnej specjalistycznej wiedzy, jedynie wyobraźni geometrycznej, spostrzegawczości i odrobiny wprawy. Świetnie nadają się na kółko matematyczna lub zajęcia na zielonej szkole.
Zadania o podziale figur na mniejsze, przystające części, przy ewentualnym zachowaniu pewnych dodatkowych warunków, często występują wśród łamigłówek matematycznych. Nie wymagają na ogół żadnej specjalistycznej wiedzy, jedynie wyobraźni geometrycznej, spostrzegawczości i odrobiny wprawy. Świetnie nadają się na kółko matematyczna lub zajęcia na zielonej szkole.
Różne połowy?
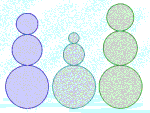 Na pewno niektórym z Was zdarzyło się oberwać burę od nauczyciela za mówienie "mniejsza połowa" lub "większa połowa". Każdy wie, że połowy są równe. Ale czy połowy mogą być RÓŻNE? Zdecydowanie tak. Zobaczcie.
Na pewno niektórym z Was zdarzyło się oberwać burę od nauczyciela za mówienie "mniejsza połowa" lub "większa połowa". Każdy wie, że połowy są równe. Ale czy połowy mogą być RÓŻNE? Zdecydowanie tak. Zobaczcie.





 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
