Każdy widział zapewne wypaczony (tzw. zwichrowany) czworokąt (jego wierzchołki nie leżą w jednej płaszczyźnie). Nie można zbudować wypaczonego trójkąta. Dlaczego? Za to można budować niby-wielościany o wypaczonych ścianach. Jak? Zobacz.
Kółko matematyczne
Wypaczone w-ściany
Karuzela (diabelski młyn)
Bez diabelskiego młyna nie może się obejść żaden szanujący się lunapark na świecie. Najstarszym jest Riesenrad na wiedeńskim Praterze, a najnowszym - London Eye. Wrocław też ma swoje wirujące koło. Przyjrzyjmy mu się z bliska. Kręci ono krzesełkami to w górę, to w dół. Pojedyncze krzesełko wymiata w przestrzeni pewną bryłę. Co to za bryła?
Koła opasane
Koła bywają wpisane w figury lub na nich opisane. Okazuje się, że koła mogą być też na figurach opasane! Jakie to koła i czym różnią się od poprzednich? Zobacz. W tekście nie ma żadnego rysunku. To wcale nie znaczy, że rysunki są tu niepotrzebne. Bądź (samo)dzielny!
Gwiazdy zegarowe - trygonometrycznie
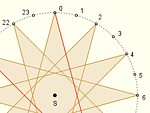Gdy wędrujemy po tarczy zegara krokiem 5 (tzn. łącząc odcinkami co piątą godzinę), dostajemy gwiazdę G (12, 5). Tę samą gwiazdę dostaniemy, chodząc po tarczy zegara 24-godzinnego krokiem 10. Tajemnice takich gwiazd odkrywaliśmy już w tekście Gwiazdy zegarowe - arytmetycznie. Tutaj zajmiemy się wyznaczaniem za pomocą trygonometrii wielkości charakteryzujących takie gwiazdy.
Gwiazdy zegarowe - arytmetycznie
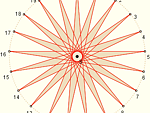Gdy wędrujemy po standardowej tarczy zegara krokiem 5 (tzn. łącząc odcinkami co piątą godzinę), dostajemy gwiazdę G (12, 5). Pobaw się tarczą zegara i zobacz, jakie inne ciekawe gwiazdy można na niej otrzymać. Zacznij od przeczytania tekstu
Gwiazdy zegarowe – geometrycznie. Okazuje się jednak, że cała tajemnica konstruowania zegarowych gwiazd tkwi w arytmetyce.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
