Wiadomo, że każdy trójkąt ma kilka środków, np. środek ciężkości, środek okręgu opisanego, środek okręgu wpisanego, punkt przecięcia prostych zawierających wysokości (tzw. ortocentrum trójkąta). Ale punktów szczególnych trójkąta jest znacznie więcej. Opowiemy o nich przy innej okazji. W tym artykule za punkty szczególne (oprócz wyżej wymienionych) uznamy jeszcze środki okręgów dopisanych do trójkąta.
Kółko matematyczne
Punkty szczególne trójkąta
Twierdzenie Ptolemeusza
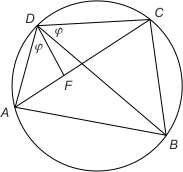Twierdzenie Ptolemeusza opisuje zależność między bokami a przekątnymi czworokąta wpisanego w okrąg. Orzeka, że iloczyn długości tych przekątnych jest równy sumie iloczynów długości przeciwległych boków tego czworokąta. Jest też prawdziwe twierdzenie odwrotne. Odkrycie tych twierdzeń i przeprowadzenie ich dowodów przypisuje się Klaudiuszowi Ptolemeuszowi (100-168) - greckiemu astronomowi, matematykowi i geografowi.
Fontanny
Przedstawione w artykule zadania są wstępem do poważnych zagadnień hydrologii i przewidywania powodzi w danym regionie. Nie uwzględniają jednak wszystkich aspektów ważnych w tym problemie, na przykład zmiennej czasu lub typu podłoża. Zatem może są tylko zabawą? Sprawdź.
Słoneczniki
Ile słonecznik ma pestek? To zależy od gatunku słonecznika. Zbadamy 6 rodzajów słoneczników, które mają nieskończenie wiele pestek. Zamiast liczyć pestki, będziemy obliczać ich łączne pole. W każdym przypadku interesować nas będzie odpowiedź na pytanie, jaka część pola jest wypełniona żółtymi pestkami.
Prezentujemy kilkanaście zadań, niektóre z przykładowymi rozwiązaniami. W wielu z nich nie jest konieczne obliczanie wymiarów pestek i można obejść się bez trygonometrii.
Kula w karnawale
Proponujemy rozwiązanie kilku zadań o objętościach karnawałowych brył. Choć znajomość trygonometrii nie jest do tego niezbędna, to użycie jej języka może nam znacznie tę pracę ułatwić.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
