 O wianuszkach płaskich pisaliśmy już w artykułach:
Wianuszki - rozgrzewka oraz Wianuszki. Przykłady wianuszków przestrzennych oglądaliśmy już w artykule Wianuszki 3D w sześcianie.
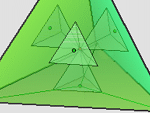
Tu zobaczymy przykłady przestrzennych wianuszków w czworościanie foremnym. Proponujemy też rozwiązanie kilku zadań.
O wianuszkach płaskich pisaliśmy już w artykułach:
Wianuszki - rozgrzewka oraz Wianuszki. Przykłady wianuszków przestrzennych oglądaliśmy już w artykule Wianuszki 3D w sześcianie.
Tu zobaczymy przykłady przestrzennych wianuszków w czworościanie foremnym. Proponujemy też rozwiązanie kilku zadań.
Kółko matematyczne
Wianuszki 3D w czworościanie foremnym
Wianuszki 3D w sześcianie
 O wianuszkach płaskich można przeczytać co nieco w artykułach
Wianuszki - rozgrzewka oraz Wianuszki. Zajrzyj tam koniecznie. Tutaj pokazujemy przykłady wianuszków przestrzennych w sześcianie. Zobacz, skąd się biorą, i rozwiąż o nich kilka zadań.
O wianuszkach płaskich można przeczytać co nieco w artykułach
Wianuszki - rozgrzewka oraz Wianuszki. Zajrzyj tam koniecznie. Tutaj pokazujemy przykłady wianuszków przestrzennych w sześcianie. Zobacz, skąd się biorą, i rozwiąż o nich kilka zadań.
Wianuszki - rozgrzewka
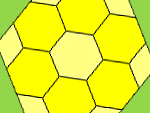 Wianuszek utworzony jest z wielokątów foremnych osadzonych na bokach większego wielokąta foremnego. Powstają wtedy bardzo ciekawe, symetryczne figury. Aż się prosi, by coś o nich porachować. Spróbuj i ty. Zaczynamy tu od prostych przykładów. Bardziej skomplikowane wianuszki znajdziesz w artykule Wianuszki.
Wianuszek utworzony jest z wielokątów foremnych osadzonych na bokach większego wielokąta foremnego. Powstają wtedy bardzo ciekawe, symetryczne figury. Aż się prosi, by coś o nich porachować. Spróbuj i ty. Zaczynamy tu od prostych przykładów. Bardziej skomplikowane wianuszki znajdziesz w artykule Wianuszki.
Największe kwakoły
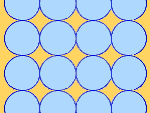 Czym jest tytułowy 'kwa-koł'? Ni to kwadrat, ni to koło. A jak wygląda? Zobacz sam. I koniecznie rozwiąż kilka zadań o kwakołach, które są umieszczone w innych figurach (trójkątach, kwadratach, półkolach i kołach).
Czym jest tytułowy 'kwa-koł'? Ni to kwadrat, ni to koło. A jak wygląda? Zobacz sam. I koniecznie rozwiąż kilka zadań o kwakołach, które są umieszczone w innych figurach (trójkątach, kwadratach, półkolach i kołach).
Konkurs Roku 2013
 Na zakończenie roku 2013 ogłaszamy konkurs dla kółek matematycznych w szkołach, klas, dla rodzin, a także dla pojedynczych uczniów, nauczycieli i pasjonatów matematyki. Wstawiając znaki działań i operacji oraz nawiasy pomiędzy cyfry numeru roku 2013, należy otrzymać kolejne liczby naturalne od 1 do jak największej. Nie może być między nimi żadnej luki. Dla rekordzistów przewidziano nagrody. Czas na przesyłania rozwiązań jest - rzecz jasna - do końca roku.
Na zakończenie roku 2013 ogłaszamy konkurs dla kółek matematycznych w szkołach, klas, dla rodzin, a także dla pojedynczych uczniów, nauczycieli i pasjonatów matematyki. Wstawiając znaki działań i operacji oraz nawiasy pomiędzy cyfry numeru roku 2013, należy otrzymać kolejne liczby naturalne od 1 do jak największej. Nie może być między nimi żadnej luki. Dla rekordzistów przewidziano nagrody. Czas na przesyłania rozwiązań jest - rzecz jasna - do końca roku.





 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
