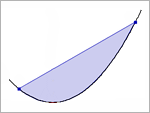
Już Archimedes potrafił obliczyć pole odcinka paraboli.
Archimedes nie rachował, jego rozumowanie było geometryczne.
Tu pokażemy, jak rachunek algebraiczny może zastąpić rozumowanie geometryczne.
Ponadto pokażemy uogólnienie dla linii y = x3.
Odlotowe figury
Odcinek paraboli (z cyklu 'Śladami Archimedesa')
Wytoczone serca
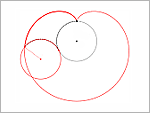Kardioida jest linią w kształcie serca. Wykreśla ją punkt brzegu koła toczącego się po nieruchomym kole o takim samym promieniu. Podobne kształty można uzyskać, tocząc inne figury. Przyjrzymy się im.
W puszce pod piłką
Do puszki w kształcie walca wpadła piłka i szczelnie w niej utknęła (bo puszka ma promień podstawy R i wysokość 2R, a piłka ma promień R). Ale w puszce pod piłką jest jeszcze trochę miejsca. Ile? Zmieszczą się tam jeszcze inne bryły. Jakie? Zobacz i rozwiąż kilka zadań.
Kule w ośmiościanie foremnym
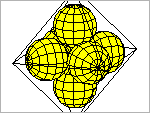Kule osadzone w ośmiościanie foremnym są prawdziwym wyzwaniem dla miłośników geometrii. Zobacz, jak wyglądają, i rozwiąż kilka zadań.
Wianuszki
Wianuszek utworzony jest z wielokątów foremnych, które osadzone są na bokach większego wielokąta foremnego. Rozmaite wianuszki mają ciekawe, symetryczne kształty. Aż się prosi, by o nich coś ciekawego porachować. Wcześniej badaliśmy już najprostsze wianuszki złożone z trójkątów równobocznych, kwadratów i sześciokątów foremnych. Zanim przeczytasz dalszy tekst i spróbujesz rozwiązać zadania zajrzyj koniecznie do artykułu Wianuszki - rozgrzewka).
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
