Kula utkwiła głęboko w ciele pacjenta... oops, tzn. w stożku. Przebiła powierzchnię i dotarła aż do serca tzn. do osi stożka. Jak wygląda ślad, który kula pozostawiła na powierzchni stożka? Zobaczcie.
Odlotowe figury
Kulą w... stożek
1 komentarz
Czytaj dalej
B(a)ryłka Archimedesa
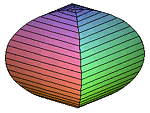Jak wygląda baryłka Archimedesa? W talii ma kwadrat, z profilu i en face jest okrągła, a jej połowa wygląda jak igloo. Zbadajmy jej różne oblicza. Ciekawe, co wspólnego miał z nią Archimedes.
Bańki w sześcianie i w komputerze
Dzięki napięciu powierzchniowemu bańki mydlane przyjmują kształty o minimalnym polu powierzchni. Bardzo interesujące są błony mydlane rozpięte na szkieletach szkieletach brył. Zachęcamy do eksperymentów. Tu zbadamy tylko powierzchnię rozpiętą na szkielecie sześcianu. Wcześniej można zrobić kilka ćwiczeń z artykułu Kolekcje trapezów w sześcianie.
[3, 4, 5] w 3D
Trójkąt prostokątny, którego boki mają długości całkowite zwykło się nazywać pitagorejskim. Taki jest np. trójkąt o bokach 3, 4, 5. Pitagorejski czworościan to taki, w którym ściany są trójkątami prostokątnymi, a krawędzie mają długości całkowite. Tylko czy taki czworościan w ogóle istnieje? Zobacz.
Kula w szkielecie
Tytuł brzmi jak zaczerpnięty z thrillera lub z kryminału. Zatem nie może zabraknąć dreszczyku emocji. Będziemy badać kule oparte na szkieletach wielościanów. Dla niektórych szkieletów takie kule nie istnieją, dla innych istnieją i są w nich zaklinowane, a dla jeszcze innych istnieją, ale swobodnie mogą z nich wypaść.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
