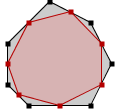
W danym wieloboku w wyznaczamy środki jego boków i widzimy, że wyznaczają one nowy wielobok. Nazwiemy go wielobokiem środków wieloboku w i oznaczymy Ś(w).
Zbadamy podstawowe własności wieloboku środków, w szczególności zależności między polem i obwodem w i Ś(w).
Odlotowe figury
Wielobok środków - pola i obwody
Równoległościan? Może tak, może nie...
Ktoś powiedział: 'Wątpić jest rzeczą ludzką', ktoś inny - 'Nic, w co wątpię, nie jest mi obce'.
Jeszcze inni mawiali: 'Wątpiący wszystkich krajów - łączcie się!'. A może coś pokręciłem? Wątpię. Spróbuj i Ty! Rozwiążemy wspólnie ciekawe zadanie o równoległoboku a może i o równoległościanie.
Na zakręcie
Zakręty bywają różne - mniej lub bardziej ostre. Mogą też mieć różne szerokości i kształty. Tu zajmiemy się najprostszymi przypadkami, utworzonymi przez krzyżujące się dwie pary prostych równoległych. Przypominają one ostry zakręt rzeki lub raczej kanału. Zbadamy, jakie maksymalnie długie żerdzie można spławiać tymi kanałami.
1 komentarz
Czytaj dalej
Zoom, zoom, zoom... i twierdzenia
Działanie operatora Hatchinsona można obejrzeć w poprzednim tekście na ten temat
(tutaj zakładamy, że Czytelnik obejrzał i zrozumiał wiele przykładów działania takich operatorów).
Teraz zastanowimy się nad tym 'co widać dalej'.
Co widać nie na obrazkach, ale poza nimi, co widać 'w nieskończoności'.
Zoom, zoom, zoom,...
Operator Hatchinsona - pod tą tajemniczą nazwą kryje się łatwy sposób otrzymywania
najprostszych fraktali. Wystarczy pomniejszać, pomniejszać, pomniejszać... .
Wbrew pozorom coś zostaje. Zobaczmy co.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
